
TFA -
Time frequency analysis
and
-modification
Software package: Version 1.040 (TFA Pure) bzw. 2.040, 16.09.16
This documentation: 16.09.16

IND - Ingenieurbüro für Nachrichten- und Datentechnik
Dr.-Ing. Peer Dahl
Keplerstrasse 44
D-75175 Pforzheim
Tel. 49-7231-650332
Fax: 49-7231-965186
eMail: P.Dahl@ind-technik.de
Internet: www.ind-technik.de
Preface
Honored customer,
honored user!
Many thanks, that you decided for this software product worldwide unique according to current research for the purpose of the time frequency analysis. As you certainly know, the special thing of this program lies in the contained algorithms (calculation methods) for the breakup of the general attachment between time and frequency resolution, which seen physical is regarded as impossible up to now.
The today available processing power allows both the development and then the use of algorithms, which denote a significant progress here. These flowed into TFA directly.
For interested: Some time-frequency analysis theory – what’s it all about?
To gain deeper insight into the frequency characteristic of signals the Discrete Fourier transform (DFT) today surely is one of the most frequent and in all fields of Digital Signal Processing used analytical tools. The spectral description of a process can in addition be starting point for purposeful manipulations in the frequency domain as a useful alternative to the processing in the time domain.
Phenomena to be examined in practice are frequently of instationary nature and are available only for a restricted time interval. Although the DFT is defined unlike the time-discrete Fourier transform only for a temporary process, the measurement period, necessary to obtain a certain frequency accuracy, can be still considerably too large. Meanwhile in case of instationary processes the minimization of the measurement period is to strive also for obtaining a satisfactory temporal localization of the result. Under these conditions the DFT supplies only a more or less indistinct estimate of the context.
Since Werner Heisenberg formulated his famous uncertainty relation of the quantum mechanics in the year 1927, also its analogy in the communication engineering therefore remained of special importance until today.
Its consequence for the spectrum analysis is that the priority between achieved frequency accuracy on the one hand and the temporal localization on the other hand is to be decided on. Both information can not be given simultaneously “exactly”. If a spectrum shall represent only a short time interval, a coarse frequency resolution is to be reckoned. If one increases the requirement onto the frequency resolution, this requires a correspondingly longer analysis time interval. The fundamental relationship between these two terms can be numerated exactly and comprehended with every spectrum analyzer - whichever the principle of operation is.
On on hand one became accustomed to this association today, on the other hand the restrictions turning out are so serious that until today worldwide endeavour is made to searched for new ways out. It is to be observed that solutions known up to now
· show disturbing side effects due to non-linearities as occurrence of cross products and phantom signals that do not exist (e.g. in case of the Wigner-Ville approach),
· do not meet the claim by a more precise consideration (e.g. in case of the Wavelet-transformation),
· to presuppose unrealistic conditions (e.g. the use of Gabor coefficients) or
· require Apriori-knowledge (e.g. Linear Predictive Coding, LPC)
and therefore their use is possible only for selected fields of application.
TFA contains a new solution, which does not have the known disadvantages or in decisively smaller extent.
Now we wish you a lot of success and new analysis epertise about your signals which never before were to be achieved in this quality.
Yours
IND - Ingenieurbüro für Nachrichten- und Datentechnik
Dr.-Ing. Peer Dahl
Keplerstrasse 44
D-75175 Pforzheim
Tel. 49-7231-650332
Fax: 49-7231-965186
eMail: P.Dahl@ind-technik.de
Internet: www.ind-technik.de
Content
2 System requirements, installation and deinstallation
2.2.1 Installation on Windows-PCs
2.2.1.2 For less practiced users
2.2.1.3 Installation of updates
2.2.2 Installation on MACs via iTunes
3.1 Start of program on Windows-PCs
4.1 The work space with the representations time domain, frequency domain and time-frequency domain
4.1.1 The representation „Time domain“
4.1.2 The representation „Frequency domain“
4.1.3 The representation „Time-frequency domain “
4.1.4 Selection and sizes of the representations
4.2.1.1.1 WAV-Format, 16 Bit, 1 channel (mono)
4.2.1.1.2 WAV-Format, 16 Bit, 2 channell (complex)
4.2.1.1.3 WAV-Format, PCM, 24 Bit and 32 Bit, 1 channel and 2 channels
4.2.1.1.4 WAV-Format, FLOAT, 32 Bit, 1 Kanal bzw. 2 Kanäle
4.2.1.1.5 TFA-Format, 32 Bit, 1 channel (real)
4.2.1.1.6 TFA-Format, 32 Bit, 2 channel (complex)
4.2.1.1.7 TXT-Format, Textfile
4.2.1.2 Export (complex) respectively Export (real)
4.2.3.1.1 Level-Colour-Assiociation
4.3.4 Presentation continuous / discrete
4.3.10 Vertikal harmonic marker
4.3.11 Horizontal harmonic marker
4.3.12 Advanced XY-Marker functions
4.3.14 Advanced zoom/boundary functions
4.3.15 Spectrum analysis settings
4.3.15.6 Further explanation of the settings
4.3.16.7 Lower level threshold
4.3.17 DDC – Digital Down Converter
4.3.17.4 Automatic setting of the DDC
5.1.1 Speech signal: F0-analysis in natural language
5.1.2 Communication engineering: FSK-signal with shift- and modulation rate measurement
5.2.1 Speech signal: Extraction of the F0-oscillation
5.2.2 Communication engineering: Extraction of a FSK-signal
5.3.1 Speech signal: Making audible a discant voice component
5.3.2 Communication engineering: Conversion of a real-valued signal into the complex base band
5.3.2.2 New TFA instance with DDC-result
5.4 Analysis of Modulation spectra
5.4.1 Selection and extraction of a frequency component as its envelope
5.4.2 Analysis of the modulation spectrum
6 FAQ – Frequently asked questions
6.1 Uncoupling XY-Marker and mouse pointer
6.2 Long duration of DXP-I-computation
6.4 Unsatisfactory spectral resolution
6.5 Staircase-shaped time signal after DDC-decimation
6.6 Installation on a network drive
9.1 Layout of the TFA-File-Format
TFA –
Time frequency analysis and -modification
1 General
Primarily the software product TFA is used for time-frequency analysis, that means the simultaneous description of a signal both in direction of the time axis as also the frequency axis. That shows a tridimensional representation, the spectrogram, at which the signal energy is colored as a third dimension characterized (e.g. high energy: red, low energy: blue to black). If the signal sample to be analyzed is something audible, one mentions the spectrogram also „sonagram”.
Whether signals, however, come from the world of audible, whether they represent physical or other scientific processes, or whether they are signals from the sundry communication engineering, e.g. the digital radio, is unimportant: In all cases conventional spectrographs can represent the time-frequency domain only with the typical uncertainty according to Heisenberg’s uncertainty relationship of communication engineering.
An example to that: In the following a speech sample[1] is analyzed with a conventional Hann-windowed fast Fourier transform (FFT) with a length of 4096:

Figure 1‑1: Speech sample, transformation FFT, FFT-length 4096
That offers a quite precise resolution into frequency direction (3,91 Hz), however, a
coarse temporal resolution (about 0,256 s). The speech pauses are very blurredly represented.
The temporal resolution can be increased through decrease of the FFT-length onto the value 512 by the factor 8 as following spectrogram shows. That offers a correspondingly coarse resolution in frequency direction (31,25 Hz), for that, however, a more precise temporal resolution (about 0,032 s). Now for example the speech pauses are more precisely represented.
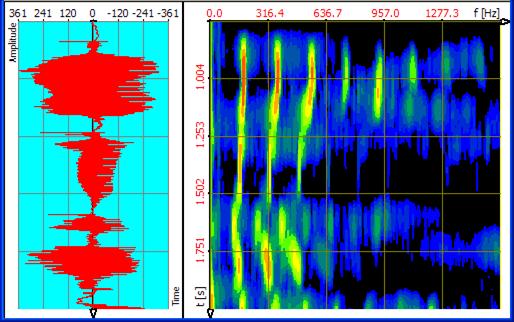
Figure 1‑2: Speech sample, transformation FFT, FFT-length 512
With TFA the signal can be exactly surveyed both in frequency- and also in time direction. That performs the new transformation method DXP-I eligible instead of the FFT. With DXP the frequency resolution (up to 4096 lines) and the time interval coming in (e.g. 512 samples) can be adjusted separately from each other as following spectrogram shows. In a way one obtains the best from the two above representations:

Figure 1‑3: Speech sample, transformation DXP-I, FFT-length 4096, 512 samples
Also a considerably more precise energy measurement is accompanied by the significantly sharper representation of the time-frequency domain because the signal energy is not distributed so very much in the plain anymore.
Based on a more precise spectrogram also the signal modification is possible in the time-frequency domain with higher quality. As described later, eligible areas can be extracted in the spectrogram or can be time-/frequency-agile filtered.
Important notice:
TFA and DXP are new, still little spread tools, that are not - that is preceded - difficult to master. However, a little bit of practice and also knowledge and experience is useful in order to be able to draw the full benefit from that. Who is not yet so familiar to DXP, the short chapter 5 “practices” is warmly recommended to. It offers an introduction and is considered as a starting point for the exploration of the own signal material.
2 System requirements, installation and deinstallation
In this section you find out, how the software TFA is put into- and removed from operation.
2.1 System requirements
The least system requirements are:
- Operation system: Windows XP (SP2) Windows Vista, Windows 7 or 8
Mac OS 10.9 Mavericks or higher
- Internet-browser for the display of help-files
- Main memory: 512 MByte
- Hard disk place: 20 MByte
- Processor clock: 2 GHz
- PC only: 1 free USB port for the dongle (copying protection stick)
TFA manages also with smaller resources, nevertheless: The higher the processor clock is, the shorter the program reaction times are, especially in the case of the DXP-transformations. A bigger main memory facilitates the enlargement of the program windows onto the faces of two monitors (dual monitoring mode) also in case of high screen resolution from 1280 x 1024 pixels. A bigger main memory also facilitates the operation with very large signal files.
Recommended is:
- Double core processor system (Dual-Core, Core Duo) with 2x3 GHz clock frequency
- 1 or 2 GB main memory
- Graphic with high resolution (1280 x 1024)
Even if TFA can currently only use one processor, in case of a multiprocessor system it is nevertheless possible to start a second instance of TFA in parallel and independently of each other. In addition the operating system reacts to other inputs more quickly, because TFA does not “block” the system.
2.2 Installation
TFA runs on MACs with OSX and PCs with Windows operation system. The installation differs because the sources of supply.
2.2.1 Installation on Windows-PCs
TFA is - how many other IND software products also are – designed in a way that it does not have to be registered in the operating system of the computer. It therefore only requires system resources when it started. Through that it does not stress the registry files, does not slowdown the operation system and does not extend the computer start time either.
TFA is delivered as a ZIP-archive. The ZIP-archive contains the folder „TFA", under that all needed subdirectories and files lie.
For the installation the ZIP-archive is to be unpacked into an arbitrary folder. To do this one extracts the complete folder „TFA" including its subdirectories and files onto an arbitrary place on the hard disk.
Notice: You must have administrator-rights!
2.2.1.1 For expert users
Please copy the contents of the ZIP archive under retention of the directory structure onto an arbitrary place of your hard disk and plug in the USB dongle into a free USB port.
2.2.1.2 For less practiced users
Maybe you wish to save the „TFA"-folders in a new subdirectory e.g. with the name „TimeFrequencyAnalysis". Please proceed then in following steps:
Step 1: Creation of a folder named „TimeFrequencyAnalysis " on the hard disk.
To that
- one opens the Windows-Explorer e.g. with the key combination „<Windows> + <E>",
- choose a folder on the wanted hard disk drive or create one at a wanted folder place by pressing of the right mouse button, then ->New->Folder. Now one enters e.g. „TimeFrequencyAnalysis" and confirms that with the „return" –Key.
Step 2: Unpack the ZIP archive into the before created folder. According to that, as you acquired the TFA-ZIP archive,
- it is stored on a storage medium or
- lies as download e.g. in your download folder or
- is managed by your download-manager-software.
Please open the ZIP-archive with a double-click with the left mouse button onto the ZIP-file or by clicking onto the key „Proceed" (or comparably similar) in your download-manager.
The indicated contents of the ZIP-archive are to be copied with the right mouse button and to be pasted into the folder created in step 1.
Possibly you would like to create further folders in the folder „TimeFrequencyAnalysis" e.g. for your signal files. In this case your directory structure looks e.g. as follows:
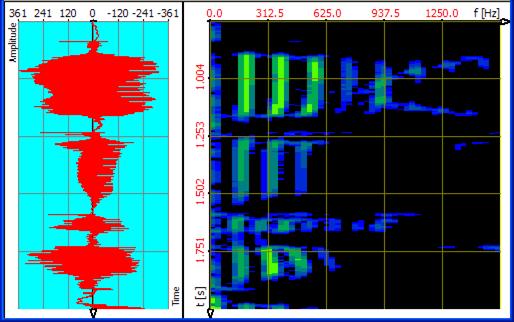
Figure 2‑1: Possible directory structure for the program installation
Step 3: Plug in the Dongle „TFA" into a free USB port.
Tip: The best choice is a USB-port on the back of the computer so that a mechanical harm of the Dongle and the computer while pushing inadvertent is avoided.
No automatic installations occur while plugging in the Dongle
2.2.1.3 Installation of updates
Please simply copy new files into the TFA-folder and hereby overwrite older files with the same name.
2.2.1.4 Deinstallation
The complete deinstallation is simple: To that
- one opens the Windows-Explorer e.g. with the key combination „<Windows> + <E>",
- chooses the folder into which the installation was performed,
- clicks with the right mouse button on it and chooses the command “delete".
2.2.2 Installation on MACs via iTunes
MAC licences are supplied by the Apple platform iTunes. Installaton and Deinstallation are done via Apple’s standard procedures.
Included in delivery are several Wav- and PDF-Files for demonstration purposes. These are stored in the folder “TFA.app”. To be able to use them one should copy them to a convenient place on the hard disk. This is done in the following steps:
- Please right-click on the file “TFA.app” in the folder “applications”.
- Choose the entry “Show content” in the context menu.
- Select to the folder „Contents->Resources“.
- Copy the Wav- and PDF-files to a convenient place on the hard disk. The manual “TFA_docu_english.pdf” can also be read from within the app.
3 Start of program
Depending on the operation system the start oft program is a bit different.
3.1 Start of program on Windows-PCs
The program is started by a double-click with the left mouse button onto the file „TFA.exe". To that one
- opens the Windows-Explorer e.g. with the key combination „<Windows> + <E>",
- selects the folder into which the installation was performed,
- carries out a double-click with the left mouse button on the file „TFA.exe ".
Notices for more convenience:
More convenient may be the one-time setup of a link on the desktop. To this one
- opens the Windows-Explorer e.g. with the key combination „<Windows> + <E>",
- selects the folder into which the installation was performed,
- performs a right-click on the file „TFA.exe" and chooses „create link” (or comparable).
- The new linking may then be pulled onto the desktop with left mouse button.
Instead of the creation of a linking one can stitch „TFA.exe" also onto the start menu. To that one
- opens the Windows-Explorer e.g. with the key combination „<Windows> + <E>",
- selects the folder into which the installation was performed,
- performs a right-click on the file „TFA.exe" and choosees and „stitch to start menu” (or comparable).
One notices, however, that in case of a deinstallation the convenience-steps are to be revoked manually (deleting desktop-linking and/or to deleting program from start menu).
3.2 Start of program on MACs
After the installation the program is usually stored in the folder “applications”. A double click on “TFA.app” opens it.
4 The TFA progam window
When starting the program the following program window is shown according to the chosen view-options:

Figure 4‑1: The TFA programm window after program start
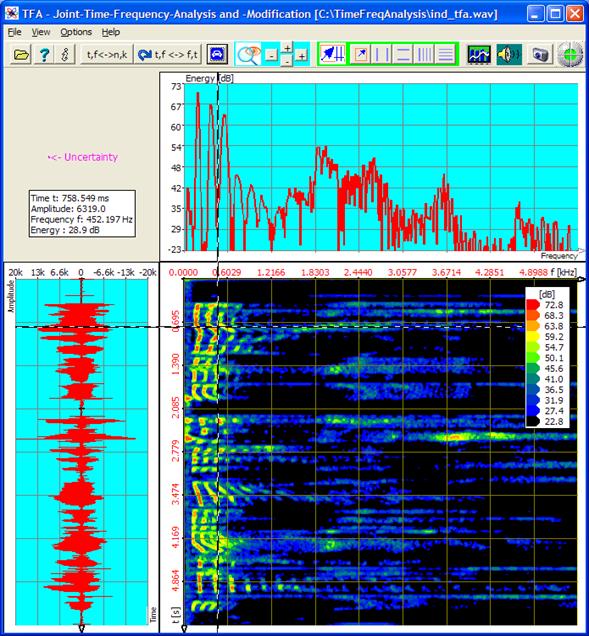
Opening e.g. the WAV-file „IND_TFA.Wav" (contained in scope of delivery, see the folders of “TFA.exe” respectively “TFA.app”) with the command “open file”, one already obtains an analysis with the representations of time domain (to the left or above), frequency domain (above and/or to the left) and the time-frequency domain (to the right - below):
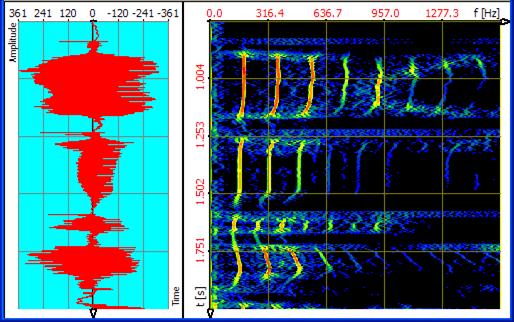
Figure 4‑2: TFA after opening file „IND_TFA.Wav“, FFT-lenght: 1024
As with most Windows-programs there is:
· The menu bar
· Short-Keys for frequently used functions and commands
· The work space, that contains the three representations time domain, frequency domain and time-frequency domain
· Next to that some measurement tools are to be seen according to the chosen options.
These program elements shall be explained now. The beginning does „The work space with the representations time domain, frequency domain and time-frequency domain”, because it allocates the biggest area in the main window.
4.1 The work space with the representations time domain, frequency domain and time-frequency domain
The figure above shows already the most important elements of the work space, the three representations:
- Time domain
- Frequency domain and
- Time-frequency domain
4.1.1 The representation „Time domain“
It corresponds to an oscillogram of a time signal. Its axes are correspondingly scaled with „time” and „amplitude". This representation type is included in many products for signal analysis and does not contain any special features. The graphic can be arranged to the left, as shown in the figure above, or arranged in the upper working area, cf. section 4.3.5.
4.1.2 The representation „Frequency domain“
This representation shows the spectrum of the time interval, whose centre corresponds to the temporal coordinate of the mouse pointer in the time-frequency representation, see below. The transformation parameters, therefore
- transformation method
- spectral- and temporal resolution
- window functions
are explained in section 4.3.15 „Spectrum analysis settings„. The graphic can be arranged upside, as shown in the figure above, or in the left of the work space, cf. section 4.3.5.
4.1.3 The representation „Time-frequency domain “
One can imagine this representation, known also as a spectrogram or in case of voice signals as sonagramm, as a common view of the frequency domain representations of all shown points in time, and that in a single graphic. The in this way necessary third coordinate could be obtained by changeover from the two-dimensional to a cube. However experiments show, that shadowing effects may hide signal components easily.
Most superior is the coloured presentation of the third coordinate to which the energy is assigned. The way energy and colour are associated is handled in section Fehler! Verweisquelle konnte nicht gefunden werden..
The graphic is always placed below/to the left in the work space, however, the axis meaning conforms to the arrangement of the other two graphics because bordering axes are common.
Usefull note:
A double-mouse-click in this representation initiates the storage of the spectral line vector (dB-scaled, txt-format) for the point of time according to the mouse position. The localization of the txt-file is the TFA working dircectory. Point of time and the frequency resolution form the file name.
4.1.4 Selection and sizes of the representations
In Figure 4‑2 a proposal for the sizes of the three representations is given. For the benefit of a certain representation it may be sometimes better to draw a graphic in a smaller way or completely to renounce it.
That is simply possible through mouse-drawing of the window boundaries. As soon as the mouse pointer is in the area of a window boundary, the typical mouse pointer symbol indicates the readiness to size the figure. The following two figures give examples:

Figure 4‑3: TFA with enlarged time-frequency representation
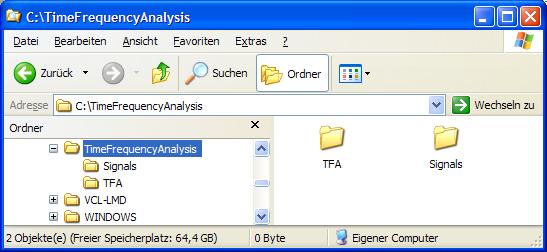
Figure 4‑4: TFA with enlarged time representation
4.2 The menu bar
![]()
The menu bar includes the points
- File
- View
- Options
- Help
The next sections pay attention to them.
4.2.1 File
It is selectable:
- Open…
- Export
- Close
4.2.1.1 Open
TFA can handle six file formats:
- WAV-Format, 16 Bit PCM, 1 channel (mono) und 2 channel (complex)
- WAV-Format, 24 Bit PCM, 1 channel (mono) und 2 channel (complex)
- WAV-Format, 32 Bit PCM, 1 Kanal (mono) und 2 channel (complex)
- WAV-Format, 32 Bit FLOAT, 1 channel (mono) und 2 channel (complex)
- TFA-Format, 32 Bit, 1 Kanal (mono, reell-wertig) und 2 channel (complex)
- TXT-Format, Textfile
In case of a stereo wave file this is turned to mono according to the choice:
Checking “L” chooses the left channel from the stereo signal, “R” gets the right channel. “L+R” mixes both channels.
And “Complex” offers the use of stereo file format to read complex signals with real part and imaginary part.
4.2.1.1.1 WAV-Format, 16 Bit, 1 channel (mono)
PCM-16-Bit is the mostly used format. Normally a signal recording will subsist as a one-channel real valued file, therefore a usual recording in mono.
4.2.1.1.2 WAV-Format, 16 Bit, 2 channell (complex)
TFA can also handle complex valued signal files. Such can arise e.g. at the output of a digital down converter (DDC) and contain a real part (Re) and an imaginary part (Im). The sample sequence within the file is (Re), (Im), (Re), (Im).... . For this two-channel file format the use of the Stereo-WAV-format has prevailed. Instead of the left-/right-Information the two channels are interpreted as real part and imaginary part. TFA cannot be used for processing stereo files.
Notice: In order to be able to process this file format still more precisely, at first a sampling rate doubling is performed in TFA. Through that the measurement properties improve, but the indicated sample numbers have the double valuation in the comparison with the file. Time and frequency reference is not affected by that of course.
4.2.1.1.3 WAV-Format, PCM, 24 Bit and 32 Bit, 1 channel and 2 channels
These formats are similar to those described in the two sections before. The difference is the use of 3 and 4 Bytes per sample to achieve a higher dynamic range.
4.2.1.1.4 WAV-Format, FLOAT, 32 Bit, 1 Kanal bzw. 2 Kanäle
This format stores each sample as a floating-point-value instead of PCM.
4.2.1.1.5 TFA-Format, 32 Bit, 1 channel (real)
This is a TFA-format which supports the following:
- Samples are stored in the format 32-bit-Float instead of having samples as 16-bit integer values. Through that in case of the signal-export and/or signal-import the otherwise always occurring conversion loss is dropped.
- The sampling rate is also stored as 32-bit-Floating point, to support very slow processes, (e.g. earth science) and also very fast ones (e.g. radio technology).
- The format includes a timestamp, so that the time-reference does not get lost due to signal extractions.
The layout of the TFA-file-format is given in chapter 9.1.
4.2.1.1.6 TFA-Format, 32 Bit, 2 channel (complex)
The same explanations are valid as in the section before.
4.2.1.1.7 TXT-Format, Textfile
Sample sequences are often given as text files. The values are written as plain text. They may represent integer numbers and/or floating point (real) ones. The values are separated by so-called „White-Space-Characters", e.g. by blanks or „returns”.
A textfile begins with 4 Info-values, followed by the samples:
- Info-value: Time of the first sample (start time)
- Info-value: Unit of the start time
- Info-value: Samplingrate or periodic time between samples
- Info-value: Unit of the samplingrate ort the periodic time.
Valid units consist of an optional multiplier and the unit. Multipliers my be:
- n 10 e -9
- u 10 e -6
- m 10 e -3
- k 10 e +3
- M 10 e +6
- G 10 e +9
Valid units are:
- s Seconds, used for the start time
- yr Year, used for the start time or the sampling rate when given as sampling interval
- Hz Hertz, used for the sampling rate
Exapmle: A series of measurement from earth science begins in the year 1958, wheras the time between two measurements is 0.0833333 years. The textfile would begin then als follows::
1958.0 yr
0.08333333 yr
315.56
315.56
315.56
317.29
317.34
316.52
315.69
………
Many other software products can export in the TXT-format so that thus an interface exists.
Notice: Text files offer the possibility to leave the restrictions of the WAV-format. If, however, it is supposed to be exported from TFA in WAV-files, attention is to be paid to not infringing the 16-, 24-, 32-bit value range because WAV-files are overdriven then. It is also to be noted, that the WAV-Format only allows sampling rates given as integers. The above described TFA-files are not affected by that.
4.2.1.2 Export (complex) respectively Export (real)
As referred in the section above, TFA can handle real- and complex-valued signals. Not necessarily for TFA, however for other applications it can be helpful to be able to convert the two formats among each other.
With this command one can render a loaded real-valued signal file into a complex-valued one and vice versa. In the first case that means a frequency band shift around the amount of half the sampling frequency and subsequent halving the sampling rate. In the second case the sampling frequency is doubled after the frequency shift. Of course the total bit rate remains unaffected, because also the number of channels is changed.
4.2.1.3 Close
This command closes TFA.
Program settings like e.g. FFT-lengths and other transformation parameters are
stored and are maintained for the next program restart. As customary, TFA
can also be closed through a click onto the red cross ![]() in the program header.
in the program header.
4.2.2 View
It is selectable
- XY-Marker
- XY-Grid
- Uncertainty area
- Level key
- Mouse coodinates
- Progress
If the entries are marked (tick), the corresponding elements are visible in the program window.
4.2.2.1 XY-Marker
The XY-marker is some cross-hairs whose point of intersection is coupled to the mouse pointer position in the time-frequency domain.
Important notice:
Sometimes this coupling is unwanted because e.g. for documentation purposes the XY marker shall stay while the mouse pointer leaves the representation. For a dissociation of the mouse pointer and the XY marker one presses the key „STRG", sometimes also called „CONTR". For the duration of the keystroke the coupling is canceled. In this case it is important that TFA is the currently active window that accepts key activations.
4.2.2.2 XY-Grid

The XY grid is a net of auxiliary lines in the time-frequency representation. The two other representations (time domain and frequency domain) are not affected by this option.
4.2.2.3 Uncertainty area
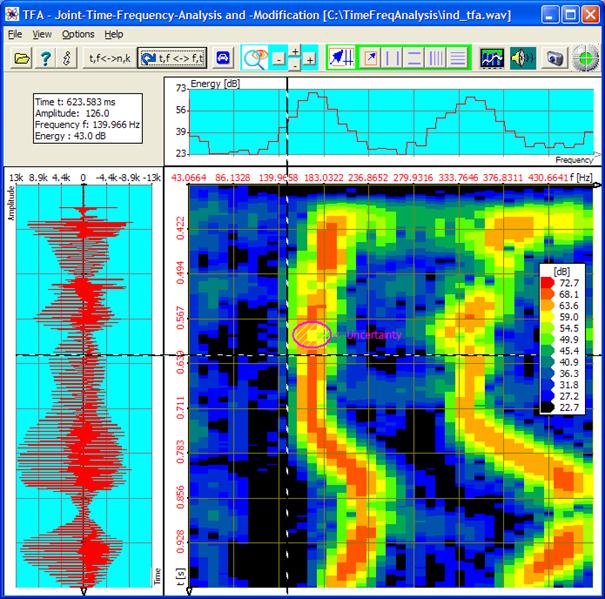
According to the uncertainty relation in the communication engineering and time-frequency analysis a precise localization in time direction stands towards a simultaneously precise localization in frequency direction. Both quantities can not be given simultaneously exactly. So there is one uncertainty of the measurement in time direction and one in frequency direction. The product of the two uncertainties stretches the uncertainty area in the time-frequency domain. A decrease of the area is desirable of course, it can be obtained by the built-in DXP-transformation methods.
In order to gain a survey of the uncertainty associated with the transformation settings quickly, TFA is endowed with a face indication. On one hand it indicates the total area in dependence of the scaling settings. And on the other hand it indicates the uncertainty distribution that mainly turns out through the size of the time signal interval coming in into the computation.
At the program start or after switching on this option the uncertainty area is arranged for instance in the middle of the time-frequency domain and magenta-coloured. It can be displaced, however, to every arbitrary point of the program window with the mouse through the left mouse button. In Figure 4‑2 the uncertainty area
![]()
is to be seen left of the spectrum (above) respectively above the time representation (left hand). The denomination „uncertainty" points at an uncertainty area with the form of a point. This point appears very concentrated, because the spectrogram shows a relatively big signal section both in frequency- and also in time direction.
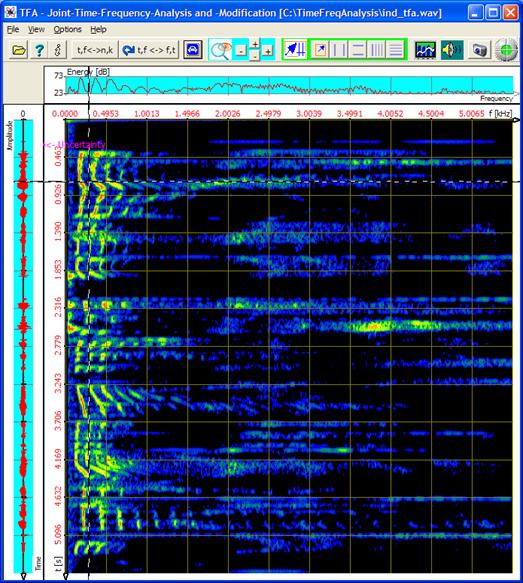
A display-zoom with the values:
- Time domain: 0.35 s to 1.0 s
- Frequency range: 50 Hz to 500 Hz
increases the detail level and in this way also the „illustration" of the uncertainty area, as following figure shows.
The uncertainty area is maybe a little difficult to be found in the coloured environment of the time-frequency domain.
Assistance: It lies a little bit right above the XY Marker cross-hairs'.

Figure 4‑5: Uncertainty area at transformation FFT, FFT-length: 1024
Caution: The physical uncertainty area is not increased due to that zoom, only its representation.
Increasing the FFT-length to e.g. the value 4096 yields to the following spectrogram:

Figure 4‑6: Uncertainty area at transformation FFT, FFT-length: 4096
The uncertainty area

has grown around the factor 4 in direction of the time axis because a four times bigger time interval comes into the calculation. In frequency direction on the other hand the size was reduced around the factor 4.
The area itself is not changed through enlargement or reduction of the FFT length, only the length distribution. One can recognize, however, at least optically by means of the two representations, that the indicated uncertainty area agrees in fact with the uncertainty of the spectrogram.
What happens now with the uncertainty area due to a selection of the transformation DXP-I?
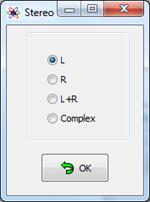
Figure 4‑7: Uncertainty area at DXP-I, resolution: 4096, time-window: 256 Samples
Also here the uncertainty area is
![]()
is arranged a little right-above the XY-Marker cross-hairs. One recognizes in agreement with the spectrogram, that
- the small magenta-coloured circle-similar face is just as extensive now in frequency direction, see Figure 4‑6, because in both cases the FFT resolution is 4096,
- however the temporal extension is reduced around the factor 8, what is associated with the reduction of the time window interval of 4096 onto 256 samples.
Nevertheless please try it out later yourselves as soon as the remaining control elements were also described here!
4.2.2.4 Level key

A spectrogram, therefore a time-frequency analysis is a tridimensional representation. The third dimension represents the energy which is colour coded. The level key, to be seen in the right middle of the spectrogram in the figures above, is an assignment table that relates colours corresponding to the energy steps.
Just like the representation of the uncertainty area the level key legend can be moved to any place of the program window with the mouse pointer by means of the left mouse button.
The setup of the level colours is freely possible, see section Fehler! Verweisquelle konnte nicht gefunden werden. “Colours”.
4.2.2.5 Mouse coordinates

If one moves the mouse pointer over the signal presentations, an information sheet indicates the signal quantities linked with the mouse coordinates. In case of the time-frequency representation that are:
- Time
- Amplitude
- Frequency
- Energy
The mouse coordinate information sheet can be moved with the mouse pointer by means of the left mouse button anywhere in the area of the program window as well.
4.2.2.6 Progress
![]()
Depending on the performance of the used computer some arithmetic operations may last a little longer. An optical control for the process progress is a turning atom which appears at the contact-place of the three signal presentations[2].
4.2.3 Options
TFA offers some options to an individual setup of the program:
- Colours
- Working directory
- Language/Sprache
- Settings
- Prog.-Start with FFT
- DC-Offset-correction
- 1.0-Scaling
The settings are stored during the closing of the program.
4.2.3.1 Colours
![]()
With this command the operation- and settings-window „Functions and parameters" is opened directly with the tab "Settings":
Figure 4‑8: Operation window „Functions and parameters->Settings “
In the upper half the colours of
- the level legend
- many program elements
can be configured.
4.2.3.1.1 Level-Colour-Assiociation
The first field „number of
level-colour-steps" is used for the setting of the colour resolution
of the energy in the time-frequency representation. The list „dB-levels"
contains as many dB-entries. Every level is separately eligible and may be
assigned a colour with the colour dialog (key ![]() ). With the key “Default” the
level-colour-association happens automatically in an intuitive color course:
). With the key “Default” the
level-colour-association happens automatically in an intuitive color course:
- High energy: Red
- …
- Low energy: Blue, black
4.2.3.1.2 Colour settings
The selection field „Colour
settings" lists all control elements that colour can be changed. Every
control element is separately eligible and may be assigned a colour with the
colour dialog (key ![]() ). With the key “Default”
the colour assignment happens automatically in the form of a colour proposal.
). With the key “Default”
the colour assignment happens automatically in the form of a colour proposal.
4.2.3.2 Working directory
![]()
There are functions in TFA which write intermediate files onto the hard disk. With this option one can pre-set the disk drive location.
(Hint: This function is not available in the MAC-Version.)
4.2.3.3 /Language/ Sprache
![]()
TFA is written in the national languages of German and English. With this option one chooses the language.
4.2.3.4 Settings
![]()
With this command the operation- and settings-window „Functions and parameters" is opened directly with the tab "Settings", see Figure 4‑8.
The settings contain graphic and transformation properties defined by the user.
Several sets of settings can be stored
and loaded with the left two keys in the lower window half. With the
right key ![]() the factory settings can be
reconstructed.
the factory settings can be
reconstructed.
4.2.3.5 Prog.-Start with FFT
During the termination of TFA all settings are stored and loaded at a renewed start of program again. In the case of the spectral transformation setting „DXP-I" that can be disadvantageous because - maybe unintentional - after opening of a signal file the slower DXP-transformation is immediately performed. This can be prohibited through marking of this option.
4.2.3.6 DC-Offset-Correction
If this option is checked a DC-offset will be removed while opening a signal file.
4.2.3.7 1.0-Skalierung
If this option is checked dependend on the file format the signals full scale is scaled to the value 1.0 while opening a signal file. So the scale is not bounded to the file format.
Example: In case of a 16-Bit-PCM-Wav-file a sample with an amplitude of 32767 will be scaled to 1.0.
4.2.4 Help
TFA offers two possibilities for assistance:
- Documentation - This command indicates this file.
- Info - Here you find the present program version and reach IND directly over an internet connection e.g. in order to search for new updates.
4.3 The short-keys
![]()
A basic principle during the development of the TFA user interface is the use of the screen area as efficient as possible. Therefore most control elements and input fields are quartered in a separate window „Functions and parameters". Saving place the short-keys offer access to the most important control elements and if necessary open the window „Functions and parameters" for advanced setting functions. Short-keys are available for following functions:
- Open
- Documentation
- Info
- Presentation continuous / discrete
- Orientation
- Automatic scaling
- Area selection
- Vertical markers
- Horizontal markers
- Vertical Harmonic marker
- Horizontal Harmonic marker
- Advanced XY-Marker functions
- „Zoom" -in and -out
- Advanced Zoom / range functions
- Spectrum analysis settings
- Play / export
- DDC - Digital Down Converter
- Graphic-export
- Status control
The functions are explained in the following.
4.3.1 Open
![]()
This command opens a signal file as described in section Fehler! Verweisquelle konnte nicht gefunden werden..
4.3.2 Documentation
![]()
The command indicates this document in the HTML-format.
4.3.3 Info
![]()
Here you find the present program version and reach IND directly via an internet connection e.g. in order to search for new updates.
4.3.4 Presentation continuous / discrete
![]()
In Digital Signal Processing the number of a sample is associated with the its sampling time [s] by means of the sampling frequency. Similar is valid for the number of a spectrum line and the represented frequency [Hz]. With this command the presentation may be switched between time [s] respectively frequency [Hz] and time sample number respectively spectrum line number. One can e.g. purposefully find a wanted sample or indicate values in its physical context.
4.3.5 Orientation
![]()
This command exchanges time and frequency axis. Figure 4‑7 would then turn as follows:

Figure 4‑9: Exchange of Orientation
4.3.6 Automatic Scaling
![]()
According to chosen signal section the level distribution can be very different. On the one hand this function adjusts the energy scaling of the time-frequency domain and the spectral representation and on the other hand the amplitude scaling so, that the diagrams are „well gained".
It is often worthwhile, to call this function also e.g. after an alternation of
- the transformation method or its parameters since due to the different uncertainty properties the existent energy is distributed over a larger or smaller area or
- the signal selection.
The in the following described control elements lie in the field
![]()
4.3.7 Area selection
![]() .
.
For many TFA-functions it is necessary to be able to select a certain signal range. The easiest possibility for the selection of a signal range is maybe the drawing of a rectangle with the mouse, similar like it is known from graphic arts software.
In order to activate this function select mode, the area selection key is to be pressed. After that selection rectangles can be stretched in all representations as following example shows.

Figure 4‑10: Area selection in the time-frequency domain
Such an area one can then e.g. enlarge (zoom), extract, export et cetera.
4.3.8 Vertical markers
![]()
Vertical markers are vertical auxiliary lines in diagrams that can be positioned there with the mouse. After pressing the key “Vertical markers” there are 2 markers (1’ and 2’) available in every representation.
The marker positions appear in a value table below the short-key-bar e.g. as follows:

Figure 4‑11: Value table for vertical markers
Apart from the marker positions also the column (2’ -1’) is to be seen. It shows the distance of the two markers.
The marker position may be adjusted with the mouse or placed exactly via entry of a wanted numerical value into the white fields.
Notice: The activation of the vertical markers deactivates other vertical markers and the area selection, see below.
4.3.9 Horizontal markers
![]()
Horizontal markers are horizontal auxiliary lines in diagrams that can be positioned there with the mouse. After pressing the key „Horizontal markers” there are 2 markers (1’ and 2’) available in every representation.
The marker positions appear in a value table below the short-key-bar comparable to Figure 4‑11: "Value table for vertical markers”, see above.
Also here is valid:
Apart from the marker positions also the column (2’ -1’) is to be seen. It shows the distance of the two markers.
The marker position may be adjusted with the mouse or placed exactly via entry of a wanted numerical value into the white fields.
Notice: The activation of the horizontal markers deactivates other horizontal markers and the area selection, see below.
4.3.10 Vertikal harmonic marker
![]()
A Harmonic-marker consists of a band of markers that are characterized by two quantities:
- Marker start - the position of the first marker of a band
- Distance – Distance of two neighbouring markers
Harmonic markers are used in order to be able to measure cyclical processes over several cycles.
An example is the measurement of a digital data stream in the case of which the bit length is constant.

Figure 4‑12: Measurement exampe with „Vertical harmonic markers“
The marker positions appear in a value table below the short-key-bar comparably Figure 4‑11: „Value table for vertical markers", see above.
One reads off that the temporal bit-distance of the frequency shift keying is 4,16 ms, which corresponds to a modulation rate of about 240 Bd. By the way: The example shows a FSK radio transmission method, where the information transmission reclines in the keying of two frequencies.
Notice: The activation of the vertical harmonic marker deactivates other vertical markers and the area selection, see below. However, the vertical harmonic marker may be combined with horizontal markers.
4.3.11 Horizontal harmonic marker
![]()
The former section explains the vertical harmonic marker. Corresponding is valid for the horizontal harmonic marker.
Notice: The activation of the horizontal harmonic marker deactivates other horizontal marker and the area selection, see below. However, the horizontal harmonic marker may be combined with vertical markers.
4.3.12 Advanced XY-Marker functions
![]()
The value table of the marker positions indicated in the main window is maybe printed in a little small way and according to the adjusted size of the graphics through insertion of so-called scroll bars unclear.
With this command or via a right click with the mouse above a graphic the operation- and settings-window „Functions and parameters" is opened directly with the tab "XY-Marker":
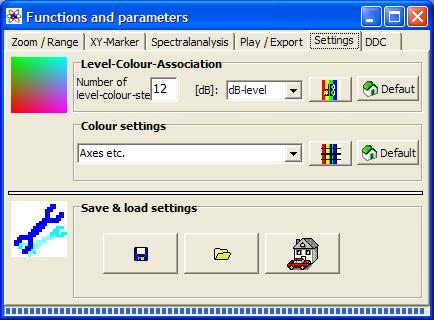
Figure 4‑13: Operation window „Functions and parameters->XY-Marker“
Here the marker positions may be read off conveniently and postponed through input of other values.
The keys above the value table correspond to the keys in the short-key-bar of the main window, cf. sections 4.3.7 “Area selection" to 4.3.11 „Horizontal harmonic marker“.
The in the following described control elements lie in the field
![]()
4.3.13 „Zoom“-in and -out
![]()
All three representations can be zoomed in or out in both their axial directions:
- Time representation: Time and amplitude
- Spectrum: Frequency and energy
- Time-frequency: Time and frequency
A zoom-in (key ![]() ) presupposes, that the new boundaries
of the indicated section are defined via markers or the area selection see,
above. With a zoom-out (key
) presupposes, that the new boundaries
of the indicated section are defined via markers or the area selection see,
above. With a zoom-out (key ![]() ) the indicated interval
doubles, increasing at both boundaries evenly.
) the indicated interval
doubles, increasing at both boundaries evenly.
There are four zoom-keys which are horizontally respectively vertically arranged. With these it can be zoomed in both directions independently by each other.
4.3.14 Advanced zoom/boundary functions
![]()
With this command the operation- and settings-window „Functions and parameters" is opened directly with the tab „Zoom / Range“:

Figure 4‑14: Operation window „Functions and parameters->Zoom / Range“
In the left field there are to see the
four zoom-keys again explained in the former section ![]() and
and ![]() .
.
In addition the window contains also
the keys ![]() and
and ![]() that are arranged diagonally. These
represent a combination of horizontal and vertical zoom.
that are arranged diagonally. These
represent a combination of horizontal and vertical zoom.
In the right field the current scalings of the indicated intervals of amplitude, time, frequency and energy are written. These fields are editable, so that a zoom can be carried out directly and precisely there.
With the help of the keys ![]() the borders of the viewed time
interval can be scrolled in the future and the past.
the borders of the viewed time
interval can be scrolled in the future and the past.
The key ![]() calls the function 4.3.6 „Automatic Scaling“.
calls the function 4.3.6 „Automatic Scaling“.
Tip: If „DXP-I" and „DXP-II" is chosen as spectral transformation method the picture buildup can last longer. Before the performing of multiple zooms it is recommended to change temporary to transformation method „FFT" in order to return at the end to „DXP".
4.3.15 Spectrum analysis settings
![]()
With this command the operation- and settings-window „Functions and parameters" is opened directly with the tab „Spektralanalysis“:

Figure 4‑15: Operation window „Functions and parameters ->Spektralanalysis“
The spectrum analysis settings and control elements include:
- Transformation
- Start
- Graphic-export
- Frequency domain with resolution and window function
- Time domain with time window and window function
These shall be explained in the following.
4.3.15.1 Transformation

Four transformation methods are available:
- FFT
- FFT with zero padding
- DXP-I (Standard)
- DXP-II (Quick)
- DXP-III (intensive)
„FFT" is the usual Fast Fourier Transform where a time interval of n samples (in the real valued case) leads to n/2 spectrum lines.
The transformation „FFT (Zero padding)" is a FFT at which for n/2 spectrum lines not n samples but base-2 power fractions of n samples go into the transformation. The samples being lacked by the FFT then are replaced by null values. A Zero-Padding-FFT offers for a certain sample number a compared to the FFT finer scanning of the frequency spectrum. However, there is no improvement of the resolution or decrease of the uncertainty.
Unlike the Zero-Padding-FFT „DXP-I“, „DXP-II“, „DXP-III“ und „DXP-IV“ are signal expanders that do not replace the missing samples with zeros, but with in fact calculated values. The different versions bring out a different trade-off between calculation time and accuracy:
- DXP-I is a good choice for general analysis (Standard).
- DXP-II calculates faster, but less precise. At signal frequencyies near DC (f = 0 Hz)
- DXP-II may calculate even more precise than DXP-I.
- DXP-III is a bit more accurate but affords double calculation time.
- DXP-IV is an older version kept for comaparision purpose.
Notice: The transformation method „(extern)" is not implemented in version V2.x yet.
4.3.15.2 Start
![]()
This key starts the calculation of the time-frequency representation. According to chosen transformation method and size of the display window this can last longer. The progress bar at the lower window border informs of the degree of the finishing.
4.3.15.3 Graphic-Export
![]()
For documentation purposes a graphic-export into other Windows application is possible as usually by pressing the key combination <ALT-Print>.
Additionally a file export is available to export the time-frequency representation as a bitmap graphics file (format „BMP”). This command opens a „File-Save-As…"-Dialog to name and save the graphics file.
The command is identical with the one described in section 4.3.18. At this place the key only increases the operating convenience.
4.3.15.4 Frequency domain
This dialog field offers settings that primarily affect the frequency domain:
- Resolution
- Window function
4.3.15.4.1 Resolution
The resolution whose value is adjustable in a selection box indicates the number of lines of a spectrum, therefore the node number of the spectrum. According to the sampling rate the frequency distance [Hz] of two neighbouring lines is joined with the line number. This value is to be seen to the right next to the selection box.
4.3.15.4.2 Window function
In the field of general spectrum analysis window functions are in common use. They weight a time interval of „resolution”-many samples. Such a window function can have in principle following figure:

Figure 4‑16: A possible window funkction for weighting a time interval
Many different types of window functions exist. In TFA some especially frequently used ones are implemented:
- „Rectangle"
- „Hamming"
- „Hann"
- „Blackman"
- „Bartlett"
These and their spectrum analysis properties are extensively described in the literature and shall not be explained here in detail therefore.
4.3.15.5 Time domain
This dialog field offers settings that apply indeed in the time domain, however, have also effect on the spectral representation. The are:
- Time interval
- Window function
4.3.15.5.1 Time interval
The time window, that is the number of samples of the time interval coming in into the transformation, is adjustable with a further selection box. In case of transformation methods like „FFT" this selection is not possible because the time interval is given by the resolution already. Other transformation methods like „FFT-(Zero-Padding)" or the „DXP"- transformation methods allow the separate choice of the time interval.
According to sampling rate a certain time interval [s] is associated with the time window size. This is to be seen to the right next to the selection box.
4.3.15.5.2 Window function
As in the case of the category „Frequency domain" there are are the same function types, see above:
- „Rectangle"
- „Hamming"
- „Hann"
- „Blackman"
- „Bartlett"
4.3.15.6 Further explanation of the settings
In TFA time-frequency analyses are possible, that are not known in the case of other products and therefore are not familiar. This section explains the analysis principle in case of the DXP-transformation methods.
Supposed:
- A signal Z exists in time domain, at which Z is defined through the choice according to section 4.3.15.5.1 “Time interval„.
- This time interval is windowed according to section 4.3.15.5.2 “Frequency domain„ e.g. with a window function of the type „Hann".
Then in the following figure the upper curve shows just this windowed time signal.
The time signal is expanded by the means of the DXP-transformations onto N values, these are to be seen in following figure in the lower curve.

Figure 4‑17: Expansion of a time interval Z (above) onto N samples (below
Figure below: The onto N-values (N = resolution according to section 4.3.15.4.1 “Resolution“) expanded time signal (red) is windowed according to section 4.3.15.4.2 “Window function" (green). The windowed time signal (blue) is transformed with the N-Points-FFT.

Figure 4‑18: Windowing of the expanded time interval at N Samples
In this manner one gets a N node spectrum that arises from a Z-samples time interval at which Z<<N is. In that a special feature of TFA lies.
4.3.16 Play / Export
![]()
With this command the operation- and settings-window „Functions and parameters" is opened directly with the tab „Play / Export“:
Figure 4‑19: Operation window „Functions and parameters ->Play / Export“
This command category is used to select signal intervals by means of the area selection or the XY-markers (see sections 4.3.7 to 4.3.9) directly in the representations
- Time domain - Selection of a time interval at full frequency bandwidth
- Frequency domain - Selection of a frequency range with complete original time interval
- Time-frequency domain - Selection of a time interval and simultaneously frequency range
and to extract it time- and/or frequency band-restricted and then
- to indicate it in a new TFA instance or
- to export it as a WAV- or TFA signal file.
During this process further signal modifications are possible if applicable.
The „Play / Export”-settings and control element include:
- Playback functions
- Inverse filter
- Envelope, magnitude
- Lower level threshold
- Speed vs. Quality
- TFA-instance
- Export
- Cancel
These shall be explained in the following. As said they presuppose a preceding area selection in one of the graphics.
4.3.16.1 Playback functions
![]()
This keypad is used to play back the selected signal range via the loudspeakers of the PC system like it is usual in many windows applications. There are the commands
- Start
- Pause
- Stop
- Back
implemented. According to selected graphics representation the computation of the signal to be played can last longer. The simple selection in the time domain is natural quickly possibly while selections in the time-frequency domain can last longer according to the size of the time interval. The progress bar at the lower window border informs of the degree of the finishing.
4.3.16.2 Envelope, magnitude
![]()
If this box is checked, TFA will calculate the signals envelope. This is used e.g. for further analysis of modulation spectra with a new TFA instance or other analysis tools.
4.3.16.3 Inverse filter
![]()
Checking this box exports the original signal except the selected interval in the time-, frequency- and time-frequency domain. The selected signal is substracted from the original.
4.3.16.4 TFA-instance
![]()
Instead of playing the selected signal via the loudspeakers of the PC system, one can start a new TFA-instance with this key. That means, a new TFA program window is opened that shows already the selected signal.
As many TFA-instances as desired can be started in parallel. Only the system resources state a limitation here of course.
4.3.16.5 Export
![]()
This command operates as the two mentioned before. The output of the selected signal is carried out as WAV- and TFA-file via a "file-save-as… "-dialog. In case of WAV there are several subformats, e.g. 16-Bit-PCM, 24-Bit-PCM, 32-Bit-PCM and 32-Bit-FLOAT.
4.3.16.6 Cancel
![]()
As already mentioned the computation of the signal extraction can last longer. With this key the process can be stopped.
4.3.16.7 Lower level threshold
In case of a selection in the representations
- time-frequency domain
- frequency domain
the specification of an absolute lower level threshold is possible. For this it is to mark the check box and to enter a wanted level threshold in the [dB]-field.
Lines with energy values below this threshold are set on the value Zero – like it is done in any case with lines outside of the selection area.
That means especially for the filtering in the time-frequency domain, that also weaker signal parts within the bandpass filter area (!) being able to be eliminated. This behavior appears as a frequency-agile bandpass filter that adjusts itself to the signal contents - a further special feature of the software TFA!
Also in case of the filter selection in the frequency domain representation this function can be useful, however, the probability for the case that all line energies are below the threshold during the entire original signal is usually considerably smaller than if the time dependence is considered additionally.
4.3.16.8 Speed vs. Quality
In the case of a selection in the representations
- time-frequency domain
- frequency domain
the adjustment of a compromise between processing speed and the achieved result quality is possible.
Check box „Use always Fast Fourier over the complete signal":
The highest speed is achieved by:
- Deactivation of a possibly chosen DXP-transformation for the benefit of the FFT-transformation
- Computation over the complete signal without considering the temporal behaviour. Notice: Then a possible chosen low level suppression can not operate time-agilely anymore. Instead of this the consideration of the average signal level occurs.
For this the check box is to be marked.
Slow / fast - control
If the above mentioned check box is not marked, also in case of DXP-transformation the speed can be increased through a single transformation supplying several samples. Through that the time reference of the transformation suffers a little which, however, mostly does not disturb because it is a question of only some ten samples.
The number of the samples used with every single transformation can be varied with the slider and thus the speed can be adjusted between „Slow" and „Fast".
4.3.17 DDC – Digital Down Converter
![]()
From version V 2.x TFA is equipped with a Digital-Down-Converter (DDC). The DDC is not available in version 1.x (Mac: TFA Pure) that is identical in other respects.
What is the primary benefit of a DDC?
The great advantage of a DDC is the possibility of sampling rate reduction. In the case of a given spectral resolution reduced signals can be surveyed more precisely in frequency direction because with the decimation of the sampling frequency the mode separation of two spectrum lines sinks. That is in particular favourable in case of the DXP-transformations because their adjustable frequency resolution is restricted on 4096 lines.
Example:
Situation: A signal sample of a physical phenomenon includes interesting signal components in the frequency range 250 kHz +/- 5 kHz. The high center frequency forces to a high sampling rate of e.g. 1 MS/s.
Consequence: Then the mode separation of two spectrum lines is about 244 Hz at a frequency resolution of 4096. So the to be examined 10 kHz frequency band is presented only through about 40 lines.
Relief: Digital-Down-Conversion of the signal with shifting down the frequency band around 245 kHz and reduction of the sampling rate from 1 MS/s to e.g. 40 kS/s. In this way the frequency resolution is about 10 Hz or rather about 1000 lines.
Therefore the DDC belongs to the indispensable equipment of a spectrum analysis system.
To support a clear arrangement of the main window, no own access point is available there for the DDC. The DDC can be obtained via the operation- and settings window „Functions and parameters” and the tab „DDC":

Figure 4‑20: Operation window „Functions and parameters ->DDC“
This command category is used to select signal intervals by means of the area selection or the XY-markers (see sections 4.3.7 to 4.3.9) directly in the representations
- Time domain - Selection of a time interval at full frequency bandwidth
- Frequency domain - Selection of a frequency range with complete original time interval
- Time-frequency domain - Selection of a time interval and simultaneously frequency range
and to extract it time- and/or frequency band-restricted and then
- to indicate it in a new TFA instance or
- to export it as a WAV- or TFA signal file.
In addition to the extraction as an ordinary time signal the calculation of the instantenous values is possible for eq. modulation spectra analysis.
The group of „DDC”-functions is related to the group „Play / export", however, there are fundamental differences. The group of „DDC”-functions is used for following operations:
- Selection of a signal range with band-pass filtering
- Frequency shift e.g. to shift of inaudible high-frequency contents into the acoustic range
- Reduction of the sampling rate for the decrease of the quantity of data and to rise of the spectral gauging accuracy
- Transformation of a real-valued signal into an analytical complex-valued one as an alternative e.g. to the Hilbert-transformation. In the complex case many methods of measurement exist which are denied to real-valued signals.
- Transformation of a complex-valued signal into a real-valued one
- Calculation of instantenous values
The „DDC”-settings and controls include:
- One /two channel file
- Mixer frequency
- Decimation factor
- Automatic DDC-setting
- Instantenous values
- TFA-instance
- Export
These shall be explained in the following. They presuppose as said a preceding area selection in one of the graphics.
4.3.17.1 One-/Zwo channels
![]()
Here it is to be specified whether the DDC result shall be real-valued or complex-valued. Complex-valued files require the setting „2".
4.3.17.2 Mixer frequency
![]()
This is the negative or positive
frequency shift a selected signal will be transposed. Depending on, whether
frequency specifications are „continuous" or „discretely" (selected
according to section 4.3.4
or the key ![]() ), one enters the frequency shift in
[Hz] or in frequency lines of the spectrum.
), one enters the frequency shift in
[Hz] or in frequency lines of the spectrum.
4.3.17.3 Decimation factor
![]()
With the selection of a frequency range a band limitation is associated. With a frequency shift towards f=0 the signal bandwidth respectively the highest occurring signal frequency is reduced again. According to the sampling theorem[3] the sampling frequency has to be only at least twice of the highest signal frequency. One can reduce the sampling frequency where appropriate. A decimation factor (> 1) may be specified in this field.
4.3.17.4 Automatic setting of the DDC
![]()
In dependence of the desired number of channels there is a usual case for which TFA can carry out the DDC- setting itself or suggest it.
- Real-valued 1- channel result file: This case describes the desire, that a selected higher frequency band is mixed down so that the lowest frequency appears in the frequency zero position. The sampling rate can be reduced then concerning the new highest signal frequency.
Example: Making audible of a signal outside the acoustic range.
- Complex-valued 2- channel result file: Here the middle of the selected higher frequency range is supposed to appear in the frequency zero position.
Example: Digital modulated communication engineering signals (ASK, PSK, FSK) which can be analyzed in complex base band situation better. The sampling rate reduction can refer to the modulation rate
Pressing the key fills the two DDC input fields.
4.3.17.5 Instantenous values
![]()
Eg. for the analysis of modulation spectra instantenous values are used instead of the time signal. Dependend on the modulation type one of the 3 options is to be marked.
4.3.17.6 TFA-instance
![]()
With this key the DDC result can be indicated in a new TFA-instance. That means, a new TFA program window is opened that shows already the selected signal.
As many TFA-instances as desired can be started in parallel. Only the system resources state a limitation here of course.
4.3.17.7 Export
![]()
This command operates as the one mentioned before. The output of the selected signal is carried out as WAV- and TFA-file written to disk via a "file-save-as… "-dialog. In case of WAV there are several subformats, e.g. 16-Bit-PCM, 24-Bit-PCM, 32-Bit-PCM and 32-Bit-FLOAT.
4.3.18 Graphic export
![]()
For documentation purposes a graphic-export into other Windows application is possible as usually by pressing the key combination <ALT-Print>.
Additionally a file export is available to export the time-frequency representation as a bitmap graphics file (format „BMP”). This command opens a „File-Save-As…"-Dialog to name and save the graphics file.
The command is identical with the one described in section 4.3.15.3. At this place the key shall only increase the operating convenience.
4.3.19 Status control
![]()
If the indication shines green, TFA is in idle status. If it shines red, computations are not finished yet. If the operation window „Functions and parameters” is opened the progress bar at the lower window border informs about the degree of the finishing.
5 Practices
TFA and DXP are new, still little spread tools, that are not - that is preceded - difficult to master. However, a little bit of practice and also knowledge and experience is useful in order to be able to draw the full benefit from that. Who is not yet so familiar to DXP, this short chapter is warmly recommended to. It offers an entrance, and is considered as a starting point for the exploration of the own signal material.
The solving of the given tasks is nonessential. More important is the practice with the functions of TFA.
Representative for the almost infinite application field of time frequency analysis some topics will be handled which maybe especially often occur in theory and practice in a comparable sense and therefore were already object and example of this documentation. They are:
Time frequency analysis
· Speech signal: F0-analysis in natural language
· Communication engineering: FSK-signal with shift- and modulation rate measurement
Filtering
· Speech signal: Extraction of the F0-oscillation
· Communication engineering: Extraction of a FSK-signal
Frequency translation
· Speech signal: Making audible a discant voice component
· Communication engineering: Conversion of a real-valued signal into the complex base band
5.1 Time frequency analysis
Purpose of this section is to show, how a first small knowledge about the signal composition changes from step to step successive to a clean overall picture. Very important is to bring up the measurement close to the border of Technical Uncertainty Relation cautiously because TFA can not unfold its strengths before then. And not till then a analysis precision will occur that is not accessible with conventional procedures.
A basic principle is derived from that:
TFA is suitable for every kind of the spectrum analysis and time frequency analysis. However, the abilities of DXP do not become visible before the signal analysis situation requires this precision. Indeed this is mostly the case at time frequency scenarios, however, if these lie far from the uncertainty relation, DXP is not necessary and the in TFA also implemented FFT equivalent. In the extreme case of the analysis of a sine continuous tone DXP does not cause any advantage compared to a FFT-analysis.
Tip 1:
To be able to graphically recognize a sharpness-/uncertainty effect at all, it is important that in TFA a time signal area became zoomed, that is so small, that the uncertainty area, cf. section 4.2.2.3 “Uncertainty area”, is clearly to see. Otherwise the uncertainty possibly may not be evaluated due to the restricted resolution of the PC monitor and the eye.
Tip 2:
At first the most important DXP-setting is the choice of the correct time interval according to section 4.3.15.5.1 “Time interval". If possible the time window size should be as large as a signal interval may be considered as stationary. Examples: A stationary signal interval can have for instance the length of a speech sound or e.g. half the bit length of a communication signal.
The FFT analysis is suited well as a Pre-analysis, in order to find out a first value for the DXP time interval and, whether there is a time-frequency analysis problem actually at all. For this one can test several FFT-lengths. If it turns out that at smaller FFT lengths a time-frequency dependant energy distribution appears, then this would be a first choice for the DXP time interval after a change to the DXP-I-transformation or DXP-II transformation method.
Tip 3:
After switching on the DXP-transformations
- one takes the just appraised time interval as a fist basis (furthermore a Hann-window is mostly a good choice),
- adjusts the frequency resolution to the same (if the frequency resolution is identical the time interval, then DXP works as FFT) and
- increases the frequency resolution successively according to section 4.3.15.4.1 “Resolution„.
Then the frequency contents should appear exactly as well.
Tip 4:
Based on the fact of this constellation one can experiment with different time interval sizes, window functions and resolutions. Thereby one pays attention to the uncertainty area which must match to the signal temporally and which then indicates the frequency-uncertainty spectrally.
With these 4 tips a TFA-DXP-time frequency analysis succeeds.
5.1.1 Speech signal: F0-analysis in natural language
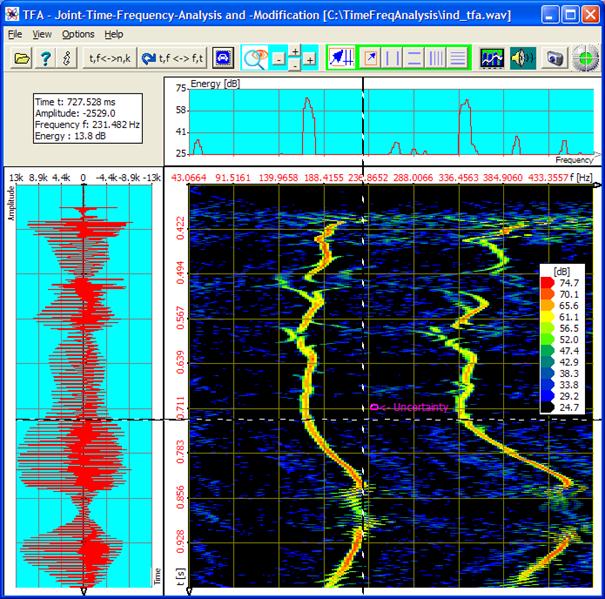
Question: Which is the fundamental frequency of the voice from file „ind_tfa.wav"
at the time t = 0,77 s?
Answer: At this time the fundamental frequency F0 is f = 188,4 Hz.
In order to obtain an answer, one can run through e.g. following steps:
1. Step – Opening the file and representing it clearly
One
- opens
the file „ind_tfa.wav”
- marks all view-options
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to
„FFT" with a resolution 1024
) the transformation method to
„FFT" with a resolution 1024 - presses the
key „Start"

- presses
the key „automatic scaling"
 at the main window
at the main window - presses
possibly the keys „Presentation continuously / discrete"
 and/or „Orientation"
and/or „Orientation" 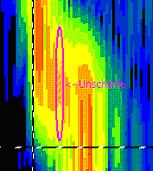
It will appear the following or a very similar program window. According to PC system the figure can differ a bit and of course e.g. the XY-marker depends on the position of the mouse pointer, and so forth.

Figure 5‑1: File „ind_tfa.wav“, FFT-analysis, resolution 1024 Points
The XY-marker is positioned already approximately at the place of interest. One reads in the area „mouse coordinates”, cf. section 4.2.2.5 “Mouse coordinates":
t = 777,052 ms f = 183,032 Hz
That is not very exactly yet, because already the restricted graphics resolution of the monitor is noticeable here. A „zoom-in" according to section 4.3.13 „Zoom“ will help. That happens in the next step.
2. Step - Zoom into the time-frequency domain’s area of interest
For that there are several possibilities:
- Direct
setting of the indicated area via the key
 , cf. section 4.3.14 “Advanced zoom/boundary
function"
, cf. section 4.3.14 “Advanced zoom/boundary
function" - area
selection
 according to section 4.3.7 and zoom
according to section 4.3.7 and zoom - use
of the „Vertical markers"
 and „Horizontal
markers"
and „Horizontal
markers"  according to sections
Fehler!
Verweisquelle konnte nicht gefunden werden. and 4.3.9
according to sections
Fehler!
Verweisquelle konnte nicht gefunden werden. and 4.3.9
The last method is maybe a little complicated, but in this case one learns the dealing with the markers, for which up to now this documentation still gave no deeper going explanation.
The markers are conveniently to move with the mouse. Here they shall be positioned, however, via keyboard inputs so that the following representations here and in this practice look homogeneous.
For the zoom
- one presses the keys
 and
and  for the activation of the
vertical and horizontal markers,
for the activation of the
vertical and horizontal markers, - one enters 0,5 s to 1,0 s as the time interval into the marker value table,
- one enters 0 Hz to 600 Hz as the frequency range into the marker value table.
That can happen directly in the program main window. Then the marker value table looks as follows, whereby only the two middle rows are of interest:

After that the program window is shown similarly as in the following figure:

Figure 5‑2: Positioning of horizontal and vertical markers
After a zoom-in the area enclosed between the markers ...

... expands over the entire time-frequency domain.
The zoom can be done with the two ![]() -keys according to section 4.3.13 or “Advanced zoom/boundary
function„
(
-keys according to section 4.3.13 or “Advanced zoom/boundary
function„
(![]() ) according to section 4.3.14. In case of the first
possibility one presses
) according to section 4.3.14. In case of the first
possibility one presses
- the two of them
 -keys in the main program window,
to arrange a vertical and a horizontal zoom into the marked area. Notice:
Possible you must click with the left mouse button somewhere into the
time-frequency domain for TFA recognizes this representation to be
adapted. The latter happens automatically during the positioning of the
markers by mouse pointers.
-keys in the main program window,
to arrange a vertical and a horizontal zoom into the marked area. Notice:
Possible you must click with the left mouse button somewhere into the
time-frequency domain for TFA recognizes this representation to be
adapted. The latter happens automatically during the positioning of the
markers by mouse pointers. - the keys
 and
and  for the deactivation of the
vertical and horizontal markers
for the deactivation of the
vertical and horizontal markers - the
key „automatic scaling"
 , to adapt the scaling
onto the new representing-area.
, to adapt the scaling
onto the new representing-area.
The result of the zoom is:
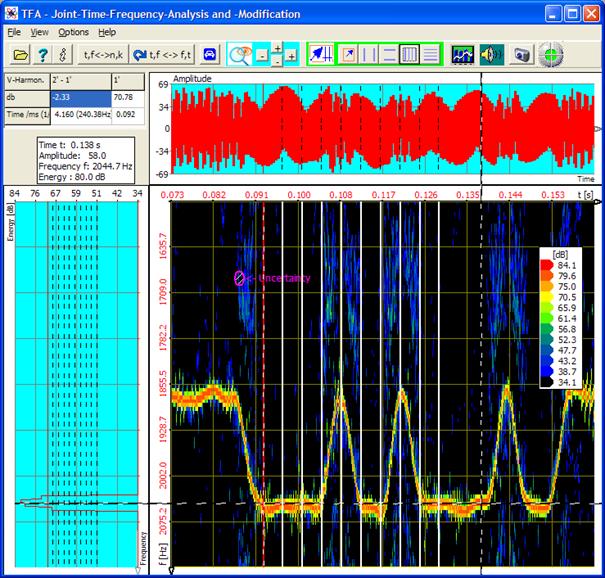
Figure 5‑3: Zoom in the time-frequency domain
One pays attention to
- the uncertainty area
 , which expresses the reliability
of the spectrogram after the zoom
, which expresses the reliability
of the spectrogram after the zoom - that now a F0- value of f = 193,799 Hz is just as plausible as the before taken value of f = 183,032 Hz. The reason lies in the FFT owning a line mode separation of 10,77 Hz during the resolution of 1024 points.
3. Step - Attempt: Rise of the measurement accuracy in time- and frequency direction
In general the measurement accuracy of the FFT may be risen through an increase of the FFT length, therefore an increase of the resolution. What happens if the FFT-resolution is increased from 1024 to the value 4096 shows following figure.
For this
- one
sets in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method
„FFT" with a resolution of now 4096
) the transformation method
„FFT" with a resolution of now 4096 - one
presses the key „Start"

- one
presses the key „Automatic scaling”
 in the main window
after finishing of the spectrogram
in the main window
after finishing of the spectrogram
The result of the higher FFT-resolution shows the figure after next. The accuracy became worse in both coordinate directions. The reason is that with the rise of the FFT-resolution the uncertainty area was changed in
![]() respectively with spectrogram set
aside
respectively with spectrogram set
aside 
Figure 5‑4: Uncertainty area at a 4096-Points-FFT
In frequency direction the uncertainty area became around the factor 4 more narrowly indeed, but in time direction four times so long. At places in the time-frequency domain where the signal frequency changes and therefore no stationarity is given anymore this FFT analysis can neither express the frequency- nor the behaviour in time.
One can find, that the rise of the FFT resolution from 1024 up to 4096 points lets become the analysis more inaccurately:

Figure 5‑5: FFT-analysis, resolution 4096 points
It is clear that therefore also the opposite which is the decrease of the FFT-resolution from 1024 to e.g. 512 points can not increase the analysis accuracy. One even tries that out by oneself!
Now it is time to turn on the DXP transformation method.
4. Step - Rise of the measurement accuracy in time- and frequency direction with DXP
In the former sections it was to be recognized that an analysis time interval of 1024 samples is at least to be preferred to a value by 4096.
- Therefore an analysis time interval of 1024 values shall serve as a start value for the DXP-analysis.
- Since DXP is only reasonable if the frequency range resolution is bigger than the value of the analysis time interval, a resolution is immediately applied by 4096.
In order to carry out the transformation correspondingly the following is to do:
One
- sets
the transformation method in the window „Functions and
parameter->Spektralanalysis” (
 ) to „DXP-I" with
a frequency resolution of 4096 lines and “Hann” as the windowing function,
) to „DXP-I" with
a frequency resolution of 4096 lines and “Hann” as the windowing function, - selects in the field “Time domain” the time interval to the value 1024 Samples and again a “Hann”-window,
- presses the
key „Start"
 and
and - presses
the key „Automatic scaling”
 in the main window
after finishing of the spectrogram.
in the main window
after finishing of the spectrogram.
The result of the DXP-transformation is to be seen in the next figure. One pays attention to
- the change of the uncertainty
area from
 to
to  , what is achieved through the
reduction of the analysis time interval,
, what is achieved through the
reduction of the analysis time interval, - that the spectrogram does still not comply to the vision according to known basics of the voice generation.

Figure 5‑6: DXP-I-analysis, resolution 4096 points, time interval 1024 samples
Now, what’s responsible for impression that the spectrogram does still not seem to be clean?
The reason is simple: The adjusted analysis time window (1024 samples) is still too big, because the pitch change in this time span is enormous. The calculated spectrum lines represent all frequency pitches that appeared.
As said at DXP the specification of the analysis time interval is independent of the specification of the frequency resolution. Therefore one can simply reduce analysis time interval.
For this the following is to be done:
- In
the window „Functions and parameter->Spektralanalysis” (
 ) – field “Time domain” one sets
the time interval to a value of 256 samples, the “Hann” window remains.
) – field “Time domain” one sets
the time interval to a value of 256 samples, the “Hann” window remains. - One
presses the key „Start"
 .
. - Again,
one presses the key „Automatic scaling”
 in the main window after
finishing of the spectrogram.
in the main window after
finishing of the spectrogram.
The result of the DXP-transformation is to be seen in the next figure.

Figure 5‑7: DXP-I-analysis, resolution 4096 points, time interval 256 samples
One pays attention to
- the change of the uncertainty
area from
 to
to  , what is achieved through the
repeated reduction of the analysis time interval,
, what is achieved through the
repeated reduction of the analysis time interval, - that now a F0-value f = 188,416 Hz is to be read quite simply and exactly.
Even more simply and more precisely the F0-measurement succeeds after a further temporal zoom. As further above described, in the following a zoom is carried out into the time interval of 0,7 to 0,84 s:

Figure 5‑8: DXP-I-analysis, resolution 4096 points, time interval 256 samples, Zoom
Along the way: The transformation DXP-II supplies similar results of analysis as DXP-I. The quality is not quite as well, for that DXP-II works considerably more quickly. Following figure shows DXP-II under the same conditions as above.

Figure 5‑9: DXP-II-analysis, resolution 4096 points, time interval 256 samples, Zoom
5.1.2 Communication engineering: FSK-signal with shift- and modulation rate measurement
Question: Which are the frequency shift and the modulation rate in the FSK-signal
given in file „ind_tfa_2.wav"?
Answer: The shift is ∆f = 170,9 Hz.
The modulation rate MR = 231,48 bd.
Notice: This signal file is complex-valued material. That means, in the format of a stereo Wav file a two channel signal is contained, at which the two channels are used for real part and imaginary part. Characteristic for complex-valued signals is that the frequency axis shows also negative frequency. The frequency range of a complex-valued signal ranges from –samplingrate/2 to +samplingrate/2. In case of real-valued signals the frequency range is 0 Hz to +samplingrate/2.
In order to achieve the answer, one can carry out e.g. following steps:
1. Step – Opening file and representing it clearly
One
- opens
the file „ind_tfa_2.wav”
 ,
, - marks all view-options,
- selects
the transformation method „FFT" in the window „Functions and
parameters->Spektralanalysis” (
 ) with a resolution of
1024,
) with a resolution of
1024, - presses the
key „Start"
 ,
, - presses
the key „Automatic scaling”
 in the main window,
in the main window, - presses
possibly the keys „presentation continuously / discrete"
 and/or „Orientation"
and/or „Orientation"  .
.
The following or a very similar program window will appear. According to PC system the figure can differ a little, and of course e.g. the XY marker depends on the position of the mouse pointer, and so forth.

Figure 5‑10: File „ind_tfa_2.wav“, FFT-analysis, resolution 1024 points
The signal section obviously contains 4 signal blocks, of which each two adjoin closely. It is presumed that the composition of the two double blocks is qualitatively identical. For the further analysis one can arbitrarily decide e.g. for the upper one.
That happens in the next step.
2. Step – Zoom into time frequency intervals
In order to select the upper double block, there are again several possibilities:
- Direct
specification of the indicated area via the key
 , cf. section 4.3.14 “Advanced zoom/boundary
function"
, cf. section 4.3.14 “Advanced zoom/boundary
function" - Area
selection
 according to section 4.3.7 with drawing of a
selection rectangle in the time domain or in the time-frequency domain and
after that zoom
according to section 4.3.7 with drawing of a
selection rectangle in the time domain or in the time-frequency domain and
after that zoom - Use
of the „Vertikal markers"
 and „Horizontal
markers"
and „Horizontal
markers"  according to sections
Fehler!
Verweisquelle konnte nicht gefunden werden. and 4.3.9
according to sections
Fehler!
Verweisquelle konnte nicht gefunden werden. and 4.3.9
Again the last method is selected with the positioning of the markers by keyboard entries so that the following representations here and in the exercise look homogeneous.
The following is to be done to zoom:
One
- presses the keys
 and
and  for the activation of the
vertical and horizontal markers,
for the activation of the
vertical and horizontal markers, - enters 0 s to 0,44 s into the marker value table as a time interval,
- enters 0 Hz to 700 Hz into the marker value table as a frequency range,
- presses the two
 -keys in the main program window,
to arrange a vertical zoom and a horizontal zoom into the marked area (Notice:
Possible you must first click anywhere into the time-frequency domain with
the left mouse button for TFA does recognize the graphic to be
adapted. The latter happens automatically during the positioning of the
markers by mouse pointers),
-keys in the main program window,
to arrange a vertical zoom and a horizontal zoom into the marked area (Notice:
Possible you must first click anywhere into the time-frequency domain with
the left mouse button for TFA does recognize the graphic to be
adapted. The latter happens automatically during the positioning of the
markers by mouse pointers), - presses once again the keys
 and
and  for the deactivation of the
vertical and horizontal marker and
for the deactivation of the
vertical and horizontal marker and - the
key „Automatic scaling"
 , to adapt the scaling
onto the new representing- area.
, to adapt the scaling
onto the new representing- area.
The result of the zoom is to be seen
in the next figure. The uncertainty area  shows that the chosen
analysis time window is much too large in respect of the present signal,
because at least the pause between the signal blocks is much shorter. Therefore
the pause is indeed to be recognized in the time domain but not in the
time-frequency domain.
shows that the chosen
analysis time window is much too large in respect of the present signal,
because at least the pause between the signal blocks is much shorter. Therefore
the pause is indeed to be recognized in the time domain but not in the
time-frequency domain.

Figure 5‑11: Representation after zoom, FFT-analysis, resolution 1024 points
Nevertheless not only the signal is affected, but the whole signal behaviour. E.g. there are never 5 dominant signal frequencies as the spectrum may give the appearance:

Figure 5‑12: Incorrect FFT-analysis due to a too big time window, resolution 1024 points
3. Step – Increase of the temporal resolution through decrease of the FFT resolution
Following is to be done to decrease the analysis time window (= decrease of the FFT-resolution):
One
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) in the field frequency domain /
Resolution the value 256 instead of 1024, the Hann windowing keeps on
existing,
) in the field frequency domain /
Resolution the value 256 instead of 1024, the Hann windowing keeps on
existing, - presses the
key „Start"
 ,
, - presses
the key „Automatic scaling”
 in the main window
after finishing of the spectrogram.
in the main window
after finishing of the spectrogram.
The result of the higher time-resolution shows the next figure:

Figure 5‑13: FFT-analysis, FFT-resolution 256 points
One sees that now the spectrogram begins to show more variations. The disposition to the smearing in time direction decreases. Naturally the frequency uncertainty increases correspondingly. Nevertheless the spectrogram still seems blurred especially in the field of the upper signal block.
Now an experiment shall show whether the detailed degree can be improved by a further increase of the temporal resolution through decrease of the FFT-resolution.
4. Strep - Further increase of the temporal resolution through decrease of the FFT resolution
E.g. the following is to be done to arrange a further decrease of the analysis time window (= decrease of the FFT-resolution):
One
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) in the field frequency domain /
Resolution the value 64 instead of 256, the Hann windowing keeps on
existing,
) in the field frequency domain /
Resolution the value 64 instead of 256, the Hann windowing keeps on
existing, - presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window
after finishing of the spectrogram.
in the main window
after finishing of the spectrogram.
The result of the higher time-resolution shows the next figure.
It is to be observed:
- For the first time the signal pause between the two signal blocks is to be recognized also clearly in the spectrogram.
- In the area of the upper signal block the smearing in time direction decreased so far that finally no continuous frequency allocations are indicated anymore.
Important: If the 5 dominant frequency components indicated in former figure would actually exist in the signal, they would keep on being preserved also after the further decrease of the FFT-resolution in the spectrogram. Maybe this statement should be considered shortly and comprehended because it is part of the parameterization strategy.
- The uncertainty in frequency direction increased again:
![]()

Figure 5‑14: FFT-analysis, FFT-resolution 64 points
Obviously for the temporal resolution of the signal an analysis time window of 64 samples (=> FFT resolution 64 points) is a good provisional value for a DXP analysis. Then not only the temporal- but also the frequency resolution will increase again.
That happens in the next step:
5. Step – Increase of the measurement accuracy in time- and frequency-direction with DXP
In the former sections it was to be recognized that an analysis time interval of 64 samples is to be preferred to a value by 256 at least.
- Therefore an analysis time interval of 64 samples shall serve as a start value for the DXP-analysis.
- Since DXP is only reasonable if the frequency domain resolution is bigger than the analysis time interval, a value is immediately applied by 2048.
In order to carry out the transformation correspondingly the following is to do:
One
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to „DXP-I"
with a frequency domain resolution of 2048 as well as Hann windowing,
) the transformation method to „DXP-I"
with a frequency domain resolution of 2048 as well as Hann windowing, - sets up the value 64 as well as also Hann-windowing in the same window in the field “time domain”,
- presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window
after finishing of the spectrogram.
in the main window
after finishing of the spectrogram.
The result of the DXP-transformation is to be seen in the next figure. One pays attention to:
- The uncertainty area has changed from
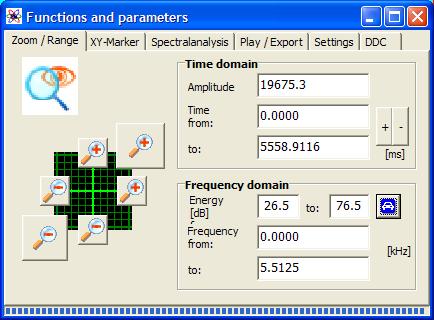 to
to  what is achieved through the
increase of the frequency resolution through DXP.
what is achieved through the
increase of the frequency resolution through DXP. - For the first time a FSK-typical spectrogram arises which represents the instantaneous frequency course.
The indicated time interval is, however, much too big in order to be able to align the FSK-signal. This may be easily changed through a temporal zoom.

Figure 5‑15: DXP-I-analysis, resolution 2048 points, time interval 64 samples
The upper signal block mainly contains a so-called REVs- sequence and therefore it may be not very interesting. Arbitrary the lower block is selected for the further measurement. That happens in the next step:
6. Step - In-Zoom into an interesting time signal section
Now it shall be demonstrated how a
mouse-supported time interval zoom can be done, keyword „Area selection” ![]() according to section 4.3.7 with drawing a selection
rectangle in the time domain or in the time-frequency domain and after that
performing a zoom.
according to section 4.3.7 with drawing a selection
rectangle in the time domain or in the time-frequency domain and after that
performing a zoom.
The following is to be done:
One
- presses the key
 , in order to obtain the area
selection mode,
, in order to obtain the area
selection mode, - draws in the time domain with the
mouse a selection rectangle around the lower signal block, for instance as
follows:

- presses the upper
 -key in the main program window,
to arrange a vertical zoom into the marked area.
-key in the main program window,
to arrange a vertical zoom into the marked area.
The following figure shows the result:

Figure 5‑16: DXP-I-analysis, resolution 2048 points, time interval 64 samples
Now one can recognize the FSK-signal sufficiently well for a measurement.
7. Step - Signal measurement
According to the task the two shift frequencies and the modulation rate are to be measured. To that are used:
- „Vertical markers" according to section Fehler! Verweisquelle konnte nicht gefunden werden.
- „Horizontal Harmonic-markers” according to section 4.3.11
The following is to be done:
One
- presses the keys
 and
and  for the activation the vertical
markers and the horizontal Harmonic markers,
for the activation the vertical
markers and the horizontal Harmonic markers, - moves the markers with the mouse pointer onto the positions to be indicated,
- reads off the measured values,
either directly in the main window’s maker value table or after pressing
of the main window key
 in the window
„Functions and parameters ->XY-Markers”:
in the window
„Functions and parameters ->XY-Markers”:

Figure 5‑17: The results given by the marker value table
Result:
- The shift frequency is 170,9 Hz.
- The modulation rate is 231,5 Bd.
Of course the result accuracy can be increased by a better choice of the zoom-intervals furthermore.
The following figure shows an example for positioning the markers for the signal measurement:

Figure 5‑18: Signal measurement
5.2 Filtering
A precise time-frequency analysis simplifies the signal filtering and signal extraction too. With the already in section 5.1 used signals that shall be demonstrated in the following.
5.2.1 Speech signal: Extraction of the F0-oscillation
In section 5.1.1 the F0-frequency was measured at a certain moment. Now the point is, to extract this oscillation and to open a new TFA program instance with it.
To that one can run through e.g. following steps:
1. Step – Opening the file and representing it clearly
One
- opens
the file „ind_tfa.wav"
 ,
, - marks all view-options,
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to
„FFT" with a resolution 1024,
) the transformation method to
„FFT" with a resolution 1024, - presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window,
in the main window, - presses
possibly the keys „Presentation continuously / discrete"
 and/or „Orientation"
and/or „Orientation"  .
.
It will appear the already shown program window Figure 5‑5, that is placed here once more. According to the PC system the figure can differ a bit, and of course e.g. the XY marker depends on the position of the mouse pointer, and so forth.

Figure 5‑19: File „ind_tfa.wav“, FFT-analysis, resolution 1024 points
From section 5.1.1 it is known that the F0-frequency was near about 180 Hz. In order to be able to recognize this frequency range better, a frequency-zoom according to section 4.3.13 „Zoom“ e.g. into the area 0...600 Hz may be helpful. That happens in the next step.
2. Step - Frequency-zoom
For that there are several possibilities:
- Direct
specification of the indicated area via the key
 , cf. section 4.3.14 “Advanced zoom/boundary
function"
, cf. section 4.3.14 “Advanced zoom/boundary
function" - Area
selection
 according to section 4.3.7 and zoom
according to section 4.3.7 and zoom - Use
of the „vertical markers"
 and the „horizontal
markers"
and the „horizontal
markers"  according to sections
Fehler!
Verweisquelle konnte nicht gefunden werden. and 4.3.9
according to sections
Fehler!
Verweisquelle konnte nicht gefunden werden. and 4.3.9
This time the first method is shall be used. To carry out the zoom the following is to do:
- One presses the key
 , the window „Functions and
parameters-> Zoom/Range" appears:
, the window „Functions and
parameters-> Zoom/Range" appears:

Figure 5‑20: Operation window „Functions and parameters ->Zoom / Range“
- One enters the frequency range of 0...600 Hz, whereon the following program main window appears:

Figure 5‑21: Frequency-zoom, FFT-analysis, resolution 1024 points
With this FFT-setting the uncertainty
in frequency direction ![]() is still quite large. That
complicates the choice of a suitable frequency section for the extraction.
is still quite large. That
complicates the choice of a suitable frequency section for the extraction.
3. Step – Increase of the frequency resolution under retention of the temporal resolution
This is possible only with the DXP-transformation method. A first approach is the choice of
- frequency resolution as 4096 points and of the
- analysis time window size as 1024 samples.
In order to carry out the transformation correspondingly the following is to do. One
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to
„DXP-I" with a frequency resolution of 4096 as well as Hann windowing,
) the transformation method to
„DXP-I" with a frequency resolution of 4096 as well as Hann windowing, - sets the time interval in the filed “time domain” to the value 1024 and again “Hann” as a window function,
- presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window
after finishing of the spectrogram.
in the main window
after finishing of the spectrogram.
The result of the DXP-transformation is to be seen in the next figure.

Figure 5‑22: DXP-I-analysis, resolution 4096 points, time interval 1024 samples
The result is still a little blurred, which has to do with the still quite big analysis time window. Therefore an analysis time window of 256 samples instead of 1024 samples alike section 5.1.1 is used next. That shows following representation:

Figure 5‑23: DXP-I-analysis, resolution 4096 points, time interval 256 samples
The F0-area is to be estimated quite good now and can be marked, without getting in contact with too many other signal parts. That happens in the next step:
4. Step - Extraction of the F0-area
The marking of the F0-area shall be
carried out freehand via the area selection ![]() according to section.4.3.7.
according to section.4.3.7.
The following is to be done:
One
- presses the key
 , in order to enter the area
selection mode,
, in order to enter the area
selection mode, - draws a selection rectangle in the time-frequency domain with the mouse around the area that is occupied by F0 - if possible, without marking the neighbouring harmonic:

- presses the key
 , to open the operation window
„Functions and parameters" directly at the register tab „Play /
export",
, to open the operation window
„Functions and parameters" directly at the register tab „Play /
export", - presses the key
 , in order to open a new TFA
instance, therefore a new TFA program window that only indicates
the selected signal. Notice: This process may take some time.
Possibilities of the acceleration are to be found in section 4.3.16.
, in order to open a new TFA
instance, therefore a new TFA program window that only indicates
the selected signal. Notice: This process may take some time.
Possibilities of the acceleration are to be found in section 4.3.16.
The following figure shows the result:

Figure 5‑24: DXP-I-Extraction at an resolution of 4096 points, time interval 256 samples
The extracted new signal contains only still the F0-frequency portions. As shown in this documentation it can be analyzed more extensively.
5.2.2 Communication engineering: Extraction of a FSK-signal
In section Fehler! Verweisquelle konnte nicht gefunden werden. the modulation parameters of a FSK-signal were analyzed. Now the point is, to extract an export a signal portion (here in the example: the second signal block) specified temporal and in its frequency.
To this one can run through e.g. following steps:
1. Strep – Opening file open and representing it clearly
One
- opens
the file „ind_tfa_2.wav"
 ,
, - marks all view-options,
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to
„FFT" with a resolution of 1024,
) the transformation method to
„FFT" with a resolution of 1024, - presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window,
in the main window, - presses
possibly the keys „Presentation continuously / discrete"
 and/or „Orientation"
and/or „Orientation"  .
.
The in section Fehler! Verweisquelle konnte nicht gefunden werden. shown program window will appear that is placed here again. According to the PC system the figure can differ a bit, and of course e.g. the XY marker depends on the position of the mouse pointer, and so forth.

Figure 5‑25: File „ind_tfa_2.wav“, FFT-analysis, resolution 1024 points
Obviously the signal section contains 4 signal blocks, of which each two are nearby.
The objective of this exercise is to extract and export the second signal block temporal and within its frequency range.
For this purpose it is at first useful to represent the block sharply. That happens in the next step.
2. Step - Precise representation of the signal block to be exported
Section Fehler! Verweisquelle konnte nicht gefunden werden. showed that the DXP-I-Analyse with a frequency resolution of 2048 points and an analysis time window of 64 samples provides a quite sharp representation of the signal.
In order to display the signal block to be exported, the following is to be done:
One
- carries on the steps according to section Fehler! Verweisquelle konnte nicht gefunden werden. up to and including step 5 again,
- presses the key
 , in order to enter area
selection mode,
, in order to enter area
selection mode, - draws a selection rectangle in the time-frequency domain with the mouse around the second signal block:
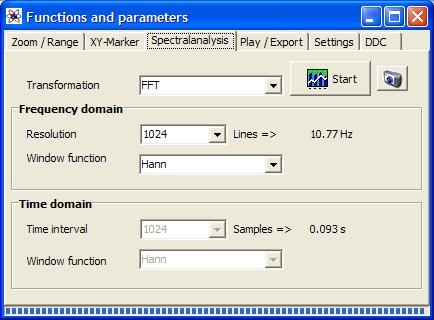
- presses the key
 , to open the operation window
„Functions and parameters" directly with the register tab „Play /
export",
, to open the operation window
„Functions and parameters" directly with the register tab „Play /
export", - presses the key
 , the output of the
selected signal is carried out via a WAV-“Saving file as… "-dialog.
Notice: This process may take some time. Possibilities for an acceleration
are to be found in section 4.3.16.
, the output of the
selected signal is carried out via a WAV-“Saving file as… "-dialog.
Notice: This process may take some time. Possibilities for an acceleration
are to be found in section 4.3.16.
5.3 Frequency conversion
The means of the TFA time-frequency analysis also simplify the frequency conversion and the extraction of signal portions. Using the signals known already from the former exercises this shall be demonstrated in the following.
5.3.1 Speech signal: Making audible a discant voice component
In this section a higher frequency band outside of the hearing distance shall be
- displaced into a lower-frequency region (frequency conversion)
- exported as a file and
- played back via the loudspeakers.
These three points are now handled in separate sections.
5.3.1.1 Frequency conversion
For this one can run through e.g. the following steps:
1. Step – Opening file and representing it clearly
One
- opens
the file „ind_tfa.wav"
 ,
, - marks all view-options,
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to
„FFT" with a resolution of 1024,
) the transformation method to
„FFT" with a resolution of 1024, - presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window,
in the main window, - presses
possibly the keys „Presentation continuously / discrete"
 and/or „Orientation"
and/or „Orientation"  .
.
It will appear the program window that is already known from Figure 5‑5. It is placed here again. According to the PC system the figure can differ a bit, and of course e.g. the XY marker depends on the position of the mouse pointer, and so forth.

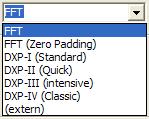
Figure 5‑26: File „ind_tfa.wav“, FFT-analysis, resolution 1024 points
The arbitrarily chosen task insists on shifting the in white encircled time-frequency area to the left nearby the zero frequency position. One estimates briefly that it is a matter of about 2 seconds of length and a frequency range of around about 2 kHz.
For the selection of a time-frequency
area there are the methods described in the sections 4.3.7 “Area selection" up to 4.3.9 “Horizontal marker„. Here the freehand
marking of the area shall be carried out via the area selection ![]() according to section 4.3.7. The following is to be
done:
according to section 4.3.7. The following is to be
done:
2. Step - Area selection and DDC
One
- presses the key
 , in order to enter the area
selection mode,
, in order to enter the area
selection mode, - draws a selection rectangle in the time-frequency domain with the mouse for instance around the area marked through the white circle:

- presses the key
 , in order to open the operation
window „Functions and parameters",
, in order to open the operation
window „Functions and parameters", - chooses the register tab
„DDC"
 , whereupon the DDC
control panel appears:
, whereupon the DDC
control panel appears:
Figure 5‑27: Operation window „Functions and parameters -> DDC“
- presses the key
 , to obtain a proposal for the
DDC settings:
, to obtain a proposal for the
DDC settings:
Figure 5‑28: DDC-setting proposal for real-valued frequency conversion
Notice How does TFA amount these setting values?
- One/two channel file: Since the chosen audio file has 1 channel, TFA acts on the assumption of „One/two channel file = 1".
- Mixer frequency: Since for instance the lower limiting frequency of the area selection is near 3 kHz, that is the shift in the direction of the zero frequency position which does not lead to a transgression of the boundary f=0 yet.
- Decimation factor: Since the width of the selected frequency band is about 2 kHz, the sampling rate may be halved through „Decimation factor = 2".
The frequency conversion takes place in the course of the file export or at handover onto a new TFA-instance.
5.3.1.2 File export
![]()
For the file export this key is to be pressed. A usual “File-save-as…”-dialog leads through the further steps. The file export can happen as a WAV file for the signal exchange to other applications or as a 32-bit TFA file together with further information, e.g. the starttime of the interval.
5.3.1.3 TFA instance
![]()
In order to open a new TFA
instance, therefore a new TFA program window that indicates only the
selected signal, this key is to be pressed. After pressing of „Automatic
scaling" ![]() the new TFA instance is
shown like as follows. Attention is to be paid to the frequency resolution that
is not 1024 but 4096.
the new TFA instance is
shown like as follows. Attention is to be paid to the frequency resolution that
is not 1024 but 4096.
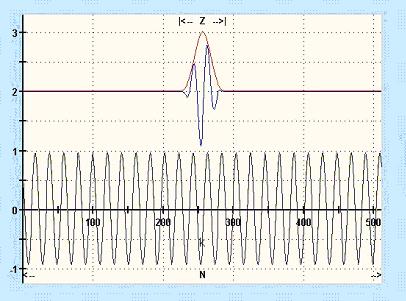
Figure 5‑29: New TFA instance with the frequency converted and decimated signal
In order to play back e.g. the entire area via speakers, one
- marks e.g. the entire time
interval in the time window to the left, while the selection mode
 is activated,
is activated, - pushes the icon
 for opening the operation window
„Functions and parameters" directly with the register tab "Play
/ export" and
for opening the operation window
„Functions and parameters" directly with the register tab "Play
/ export" and - uses the keys in usual manner
 .
.
The playback of signal intervals is detailed described in section 4.3.16 “Play / Export".
5.3.2 Communication engineering: Conversion of a real-valued signal into the complex base band
In section Fehler! Verweisquelle konnte nicht gefunden werden. it was to be seen that the signal sample „ind_tfa_2.wav" in fact represents a modulation signal from the communication engineering. It is given in an intermediate frequency band (ZF, IF), what makes possible the real-valued (one channel) storage.
For many methods of analysis, as e.g. the instantaneous value analysis, the complex baseband instead of the intermediate frequency band is more favourable. This requires the complex-valued (two channel) signal storage since in this case in addition to the so-called real part there is the so-called imaginary part.
The transformation of a real signal or complex valued signal section (like in this case) into a complex signal is object of this section.
For this one can run through e.g. following steps:
1. Step – Opening file and representing it clearly
One
- opens
the file „ind_tfa_2.wav "
 ,
, - marks all view-options,
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to
„FFT" with a resolution of 1024,
) the transformation method to
„FFT" with a resolution of 1024, - presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window ,
in the main window , - presses
possibly the keys „Presentation continuously / discrete"
 and/or the key
„Orientation"
and/or the key
„Orientation"  .
.
It will appear the program window shown in section Fehler! Verweisquelle konnte nicht gefunden werden. that is here placed again. According to the PC system the figure may differ a bit and of course e.g. the XY marker depends on the position of the mouse pointer, and so forth.

Figure 5‑30: File „ind_tfa_2.wav“, FFT-analysis, resolution 1024 points
The center frequency is about f=390 Hz. The bandwidth, that show the vertical markers, is about BB = 800 Hz, cf. following figure:
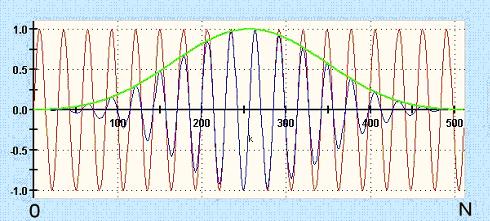
Figure 5‑31: Center frequency and bandwidth of a communicatin signal
That with the vertical marker enclosed frequency band is now to be mixed to the left into the zero frequency position that the center frequency coincides with the frequency of f=0.
2. Step - Area selection and DDC
- If the positioning of the vertical markers took place in the spectrum (upper window), the signal is thus selected, which means that a signal modification affects the entire signal within a given time. The area selection is thus already carried out.
- One presses the key
 , in order to open the operation
window "Functions and parameters".
, in order to open the operation
window "Functions and parameters". - One chooses the register tab
„DDC"
 , whereupon the DDC
control panel appears, and presses the key
, whereupon the DDC
control panel appears, and presses the key  , to obtain a proposal for the
DDC settings:
, to obtain a proposal for the
DDC settings:

Figure 5‑32: DDC-setting proposal for complex baseband
Notice How does TFA amount these setting values?
- One/two channel file: Since the chosen audio file has two channels TFA acts on the assumption of „One/two channel file = 2".
- Mixer frequency: Since for instance the center frequency of the area selection is near 378 Hz, that is the shift in the direction of the zero frequency position balanced to f=0.
- Decimation factor: Since the width of the selected frequency band is about 800 Hz, the sampling rate may be halved through „Decimation factor = 3".
The frequency conversion takes place in the course of the file export or at handover onto a new TFA-instance.
5.3.2.1 File export
![]()
For the file export this key is to be pressed. A usual “File-save-as…”-dialog leads through the further steps. The file export can happen as a WAV file for the signal exchange to other applications or as a 32-bit TFA file together with further information like the starttime of the interval.
5.3.2.2 New TFA instance with DDC-result
![]()
In order to open a new TFA
instance, therefore a new TFA program window that indicates only the
selected signal, this key is to be pressed. After pressing of „Automatic
scaling" ![]() the new TFA instance is
shown like as follows:
the new TFA instance is
shown like as follows:

Figure 5‑33: New TFA-Instanz with a signal in the complex baseband
At the beginning it was found, that the center frequency lay at about f=390 Hz. In the figure above it can be read off that now after frequency conversion it is near about 16 Hz. That means, that a value of -390 Hz as the “Mixer frequency” in the DDC control panel would have centred the signal better.
5.4 Analysis of Modulation spectra
The characteristic sound of e.g. music instruments or the human speech also comes from the modulation of the included frequency components. They are responsible for a sounds liveliness and allow us, e.g. to distinguish different violin fabricats or speekers.
This section gives an example for possible steps of an modulation spectra analysis based on a sample of a singing bowl (in german called “Klangschale”):
- Selection and extraction of a frequency component as its envelope
- Analysis of the modulation spectrum
At this place sincere thanks are given to the company „Synotec Psychoinformatik GmbH, Geyer“ for the retrieval of the signal “Klangschale.wav” that ist included in TFAs samples.
5.4.1 Selection and extraction of a frequency component as its envelope
To do this on may perform the following steps:
1. Step – Assure, that the option “DC-Offset-Correction” is set
With regard to the later calculation of the signals envelope and its spectrum this is not necessary but advantageous it TFA doesn’t start with this option set right from start.

The reason is, that the magnitude
always includes a mostly uniteressting DC-Offset which may lead to a dominate
spectral line at the frequency 0 Hz without informative value. This may compromise
the automatic scaling ![]() , because it has to regard
the 0-Hz-Peak.
, because it has to regard
the 0-Hz-Peak.
If the option is not set, one should do this, then close TFA and start again. When the program is closed many settings like the “DC-Offset-Correction” are saved and do not need to be controlled after a new start.
2. Step – Open wav-file and present it clearly arranged
One
- opens
the file “Klangschale.wav”

- marks all view options
- sets
in the window „Functions and parameters->Spektralanalysis” (
 ) the transformation method to
„FFT" with a resolution of 8192,
) the transformation method to
„FFT" with a resolution of 8192,
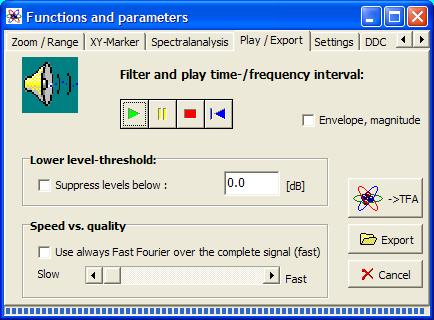
- presses the
key „Start"
 ,
, - presses
the key „Automatic scaling"
 in the main window ,
in the main window , - presses
possibly the keys „Presentation continuously / discrete"
 and/or the key
„Orientation"
and/or the key
„Orientation"  .
.
It will appear the following program window. According to the PC system the figure may differ a bit and of course e.g. the XY marker depends on the position of the mouse pointer, and so forth.

Figure 5‑34: TFA after opening the signal “Klangschale.wav”
The signals energie is mainly located in the frequency range up to about 4 kHz. A first zoom enhances the overview.
One
- presses
the button
 to enter the area
selection mode
to enter the area
selection mode - draw a selection area rectangle in the frequency domain to mark the main energy range,

- presses the right button
 in the field
in the field  to perform a horicontal zoom in
frequency direction,
to perform a horicontal zoom in
frequency direction, - presses the button “Automatic
Scaling”
 what may enhance the
view.
what may enhance the
view.
Now the program window should look like:

Figure 5‑35: Zoom in frequency range
No the spectrum of the singing bowl is more considerable.
In the following the arbitrary goal is setted to obtain the modulation spectrum of the red coloured overtone and therefore to mark and to export its magnitude signal.
3. Step – Marking the frequency componet and exporting the magnitude signal
The marking of the frequency component again my be done like shown above or
- with the vertical markers
 ,
, - that can be moved freehand or via entering the exact positions in the table (please regard the units).

Now the frequency range 350 Hz to 500 Hz is selected. Of course the selection can also be done in the time-/frequency domain.
- One presses nun the button
 to open the in the window
„Functions and parameters“.
to open the in the window
„Functions and parameters“. - One chooses the card „DDC“
 , the DDC-control panel appears.
Press the button
, the DDC-control panel appears.
Press the button
 to obtain a settings
recommendation:
to obtain a settings
recommendation:
Figure 5‑36: DDC settings recommendation
Note: How does TFA calculate this settings?
- One/two channels: Because the given wave-file is a 1-channel-file TFA will propose this.
- Mixer frequency: Because the lower cut-off frequency of the selected range is about 347 Hz, this is the shift towards the Zero-pitch f=0.
- Decimation factor: The upper cut-off frequency of the selected range is about 500 Hz, die lower at about 350 Hz. So the frequency band is about 150 Hz wide and the minimum sampling rate is 300 Hz. The actual sampling rate is 22 kHz, that leads to a rounded decimation factor of 72.
- Check the field
 because not the signal but its
envelope shall be examinded.
because not the signal but its
envelope shall be examinded.
The frequency conversation is performed with the file export ort the handover to a new TFA-Instance. The last shall now be shown.
File export (not relevant for next explanations)
![]()
In order to perform a file export this button is to be pressed. A common “Save as...“-dialogue leads to the further steps. A file export can be done as WAV-file for the exchange with other applications or as 32-Bit-TFA-file together with other information, e.g. the starttime of a signal interval.
New TFA-Instance showing the DDC-result
![]()
To open an new TFA-Instance, then
a new TFA-program window, that shows only the selected signal, this button
is to be pressed. After pressing the button “automatic scaling” ![]() the new TFA-Instance looks like
the next but one figure:
the new TFA-Instance looks like
the next but one figure:
If there are major differences probably the reason is the setting of the FFT-resolution, see settings window:
Figure 5‑37: FFT setting

Figure 5‑38: Modulations spectrum of the selected overtone
Note:
Because of setting the DC-Offset-Option one sees a magnitude signal without DC-offset. So there are negative values too.
5.4.2 Analysis of the modulation spectrum
With
the harmonic markes one finds the modulation frecuency to be  3.29 Hz.
3.29 Hz.

Figure 5‑399: Measuring the modulations spectrum with harmonic markers
6 FAQ – Frequently asked questions
This section answers questions to TFA which came up by the time. According to version of this text the list is not very long yet.
6.1 Uncoupling XY-Marker and mouse pointer
Question: How can I achieve that the XY-marker stands still and does not follow the mouse pointer?
Answer: If the TFA program window is active one presses the <Strg>-Taste. Then only the mouse coordinates are changed in case of mouse pointer movement, the XY marker stands still.
6.2 Long duration of DXP-I-computation
Question: During the start of the DXP-I-computation with a high frequency resolution it takes many seconds until the first lines are drawn.
Answer: During the change to the DXP-I-transformation method or change of the DXP- settings first of all it is carried out the computation of a matrix. At this time the red status lamp glows and the software does not seem to react. One waits this time span, after that the reaction time is nearly zero.
6.3 View elements unvisible
Question: Although the view element „uncertainty area" is visibly marked, is not to be seen in the program window.
Answer: The view elements can be moved with the mouse pointer in the area of the program window. It can happen, that they screen themselves. That also happens, when the marker and so that the marker value tables are turned on. Also they can screen view elements, when latter are in the table area. One deactivates markers and view elements and places the elements so that they do not collide. The „uncertainty area" can be placed to its origin position by switching it off and on again.
6.4 Unsatisfactory spectral resolution
Question: Using the spectral transformation method DXP-I my with a sampling rate of 10 MHz recorded measurement signal cannot be spectrally analyzed fine enough because, there is a maximum resolution of only 4096 lines, what leads to a line mode separation of more than 2441 Hz.
Answer: In DXP the maximum frequency resolution is restricted to the value 4096, because higher values would provoke a quadratic increasing of the computing duration and also a higher memory requirement. There are, however, two ways out:
- Use of the transformation method FFT with however the disadvantage of larger uncertainty
- Use of the transformation method DXP and use of the Digital Down Converter (DDC) according to section 4.3.17 for the selection of interesting signal sections of smaller frequency interval width. The increase of the Measurement accuracy corresponds to the chosen DDC decimation factor.
6.5 Staircase-shaped time signal after DDC-decimation
Question: After the use of the DDC with reduction of the sampling rate the time signal appears rough and staircase-shaped.
Answer: Even if the DDC decimation factor is correctly adjusted so that the sampling rate at least corresponds to the double of the highest signal frequency according to the sampling theorem nevertheless that means that the highest frequency components show only few samples per period. Curves can be represented no more. If this is essential, however, one simply reduces the DDC decimation factor.
6.6 Installation on a network drive
Question: Is it possible to install TFA on a network drive?
Answer: Yes, but the network drive must be addressable via a drive letter comparable to local drives. Apart from this it is to be considered that if several persons use the software simulanously the functions Playback and DDC are only constricted available.
7 Abbreviations
ARQ Block transfer technique of the telecommunication engineering
ASK Radio transmission technique, Amplitude-Shift-Keying
DDC Digital-Down-Converter
DFT Discrete Fourier Transformation
FFT Fast Fourier Transformation
FSK Radio transmission technique, Frequency-Shift-Keying
HF High frequency
IF Intermediate frequency (IF): The intermediate frequency band is
the result from down-converting e.g. a radio frequency band.
JTFA Joint-Time-Frequency Analysis
LPC Linear Predictive Coding,
NF Low frequency
PSK Radio transmission technique, Phase-Shift-Keying
REVs-Folge Reversal-Folge, 0101…-Bitsequence
TFA Time-Frequency Analysis
USB Universal Serial Bus
ZF German for “IF”: Intermediate frequency (IF): The
intermediate frequency band is the result from down-converting
e.g. a radio frequency band.
8 Table of figures
Figure 1‑1: Speech sample, transformation FFT, FFT-length 4096
Figure 1‑2: Speech sample, transformation FFT, FFT-length 512
Figure 1‑3: Speech sample, transformation DXP-I, FFT-length 4096, 512 samples
Figure 2‑1: Possible directory structure for the program installation
Figure 4‑1: The TFA programm window after program start
Figure 4‑2: TFA after opening file „IND_TFA.Wav“, FFT-lenght: 1024
Figure 4‑3: TFA with enlarged time-frequency representation
Figure 4‑4: TFA with enlarged time representation
Figure 4‑5: Uncertainty area at transformation FFT, FFT-length: 1024
Figure 4‑6: Uncertainty area at transformation FFT, FFT-length: 4096
Figure 4‑7: Uncertainty area at DXP-I, resolution: 4096, time-window: 256 Samples
Figure 4‑8: Operation window „Functions and parameters->Settings “
Figure 4‑9: Exchange of Orientation
Figure 4‑10: Area selection in the time-frequency domain
Figure 4‑11: Value table for vertical markers.
Figure 4‑12: Measurement exampe with „Vertical harmonic markers“
Figure 4‑13: Operation window „Functions and parameters->XY-Marker“
Figure 4‑14: Operation window „Functions and parameters->Zoom / Range“
Figure 4‑15: Operation window „Functions and parameters ->Spektralanalysis“
Figure 4‑16: A possible window funkction for weighting a time interval
Figure 4‑17: Expansion of a time interval Z (above) onto N samples (below
Figure 4‑18: Windowing of the expanded time interval at N Samples
Figure 4‑19: Operation window „Functions and parameters ->Play / Export“
Figure 4‑20: Operation window „Functions and parameters ->DDC“
Figure 5‑1: File „ind_tfa.wav“, FFT-analysis, resolution 1024 Points
Figure 5‑2: Positioning of horizontal and vertical markers
Figure 5‑3: Zoom in the time-frequency domain
Figure 5‑4: Uncertainty area at a 4096-Points-FFT
Figure 5‑5: FFT-analysis, resolution 4096 points
Figure 5‑6: DXP-I-analysis, resolution 4096 points, time interval 1024 samples
Figure 5‑7: DXP-I-analysis, resolution 4096 points, time interval 256 samples
Figure 5‑8: DXP-I-analysis, resolution 4096 points, time interval 256 samples, Zoom
Figure 5‑9: DXP-II-analysis, resolution 4096 points, time interval 256 samples, Zoom
Figure 5‑10: File „ind_tfa_2.wav“, FFT-analysis, resolution 1024 points
Figure 5‑11: Representation after zoom, FFT-analysis, resolution 1024 points
Figure 5‑12: Incorrect FFT-analysis due to a too big time window, resolution 1024 points
Figure 5‑13: FFT-analysis, FFT-resolution 256 points
Figure 5‑14: FFT-analysis, FFT-resolution 64 points
Figure 5‑15: DXP-I-analysis, resolution 2048 points, time interval 64 samples
Figure 5‑16: DXP-I-analysis, resolution 2048 points, time interval 64 samples
Figure 5‑17: The results given by the marker value table
Figure 5‑18: Signal measurement
Figure 5‑19: File „ind_tfa.wav“, FFT-analysis, resolution 1024 points
Figure 5‑20: Operation window „Functions and parameters ->Zoom / Range“
Figure 5‑21: Frequency-zoom, FFT-analysis, resolution 1024 points
Figure 5‑22: DXP-I-analysis, resolution 4096 points, time interval 1024 samples
Figure 5‑23: DXP-I-analysis, resolution 4096 points, time interval 256 samples
Figure 5‑24: DXP-I-Extraction at an resolution of 4096 points, time interval 256 samples
Figure 5‑25: File „ind_tfa_2.wav“, FFT-analysis, resolution 1024 points
Figure 5‑26: File „ind_tfa.wav“, FFT-analysis, resolution 1024 points
Figure 5‑27: Operation window „Functions and parameters -> DDC“
Figure 5‑28: DDC-setting proposal for real-valued frequency conversion
Figure 5‑29: New TFA instance with the frequency converted and decimated signal
Figure 5‑30: File „ind_tfa_2.wav“, FFT-analysis, resolution 1024 points
Figure 5‑31: Center frequency and bandwidth of a communicatin signal
Figure 5‑32: DDC-setting proposal for complex baseband
Figure 5‑33: New TFA-Instanz with a signal in the complex baseband
Figure 5‑34: TFA after opening the signal “Klangschale.wav”
Figure 5‑35: Zoom in frequency range
Figure 5‑36: DDC settings recommendation
Figure 5‑38: Modulations spectrum of the selected overtone
Figure 5‑39: Measuring the modulations spectrum with harmonic markers
9 Annex
9.1 Layout of the TFA-File-Format
The TFA-format supports the following:
- Samples are stored in the format 32-bit-Float instead of having samples as 16-bit integer values. Through that in case of the signal-export and/or signal-import the otherwise always occurring conversion loss is dropped.
- The sampling rate is also stored as 32-bit-Floating point, to support very slow processes, (e.g. earth science) and also very fast ones (e.g. radio technology).
- The format includes a timestamp, so that the time-reference does not get lost due to signal extractions.
The layout of the TFA-file-format is given as follow. It consists of:
- Header-Block including the above mentioned parameters
- Sequence of the Samples
The Header-Block is defined as:
// Header-Block des TFA-Dateiformats
typedef struct TFAInfo_pattern_type
{
char pcFormatKennung[20]; // Text: "TFA-Format"
long lBitzahl; // Bei TFA immer 32 (32 Bit)
long lKanalzahl; // 1: reelle Datei, 2: komplex
float fSamplingrate; // Abtastrate in Hz
long lAbtastwertezahl; // Anzahl reeller o. komplexer Samples
long lSkalaInJahren; // 1, für geophysikalische Zwecke
float fStartzeitoffset; // Das 0-te Sample entstand zu
// dieser Zeit
char pcEinheitStringStart[10]; // Einheit der Startzeit
char pcEinheitStringSampl[10]; // Einheit der Samplingrate
long lInstanznummer; // Wieviele TFA-Instanzen aktiv?
char pcZusatzinfo[100]; // Nicht benutzt
float fErsatzFloat1; // Erstzwerte für Zukünftiges
float fErsatzFloat2; // Nicht benutzt
float fErsatzFloat3; // Nicht benutzt
long lErsatzLong1; // Nicht benutzt
long lErsatzLong2; // Nicht benutzt
long lErsatzLong3; // Nicht benutzt
} TFA_HeaderInfo_type;
After the Header-Block the samples follow. In case of complex-valued files the sequence is Re[0], Im[0], Re[1], Im[1], …. , Re[lAbtastwertezahl-1], Im[lAbtastwertezahl-1].
- This page is intentionally left blank -